
分析 根据三角函数值及负指数幂化简x、y的值,根据完全平方公式及平方差公式化简整式,再将x、y的值代入可得.
解答 解:∵x=(-cos60°)-1=(-$\frac{1}{2}$)-1=-2,y=-sin30°=-$\frac{1}{2}$,
∴[4(xy-1)2-(xy+2)(2-xy)]÷$\frac{1}{4}$xy
=[4(x2y2-2xy+1)-(22-x2y2)]•$\frac{4}{xy}$
=(4x2y2-8xy+4-4+x2y2)$•\frac{4}{xy}$
=(5x2y2-8xy)$•\frac{4}{xy}$
=20xy-32
=20×(-2)×(-$\frac{1}{2}$)-32
=-12.
点评 本题主要考查整式的化简求值能力,根据三角函数值及负整数指数幂化简x、y的值是基本,准确化简整式是关键.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:解答题
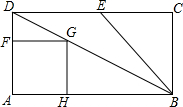 如图,在矩形ABCD中,AD=3,AB=6,E为CD边中点,F为AD上一点,以AF为边作正方形AFGH,使正方形AFGH和矩形ABCD在AD的同侧,且正方形AFGH的顶点G恰好落在对角线BD上,将正方形AFGH以每秒一个单位的速度沿射线AB方向平移,记平行中的正方形AFGH为正方形A′FGH,当点A′与点B重合时停止运动,设运动的时间为t(t≥0).
如图,在矩形ABCD中,AD=3,AB=6,E为CD边中点,F为AD上一点,以AF为边作正方形AFGH,使正方形AFGH和矩形ABCD在AD的同侧,且正方形AFGH的顶点G恰好落在对角线BD上,将正方形AFGH以每秒一个单位的速度沿射线AB方向平移,记平行中的正方形AFGH为正方形A′FGH,当点A′与点B重合时停止运动,设运动的时间为t(t≥0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,且BE=2AE,已知AD=3$\sqrt{3}$,tan∠BCE=$\frac{\sqrt{3}}{3}$,那么CE等于( )
如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,且BE=2AE,已知AD=3$\sqrt{3}$,tan∠BCE=$\frac{\sqrt{3}}{3}$,那么CE等于( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$-2 | C. | 5$\sqrt{2}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
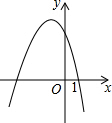 二次函数y=ax2+bx+c的图象如图所示,则化简二次根式$\sqrt{(a+c)^{2}}$+$\sqrt{(b-c)^{2}}$的结果是( )
二次函数y=ax2+bx+c的图象如图所示,则化简二次根式$\sqrt{(a+c)^{2}}$+$\sqrt{(b-c)^{2}}$的结果是( )| A. | a+b | B. | -a-b | C. | 2b-c | D. | -2b+c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
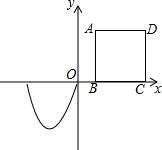 如图,在平面直角坐标系中,抛物线C1;y=ax2+bx的最低点的坐标为(-$\frac{5}{3}$,-$\frac{25}{8}$),边长为2的正方形ABCD的边BC在x轴上,点B的坐标为($\frac{2}{3}$,0),先将抛物线C1绕点O顺时针旋转180°得到抛物线C2.
如图,在平面直角坐标系中,抛物线C1;y=ax2+bx的最低点的坐标为(-$\frac{5}{3}$,-$\frac{25}{8}$),边长为2的正方形ABCD的边BC在x轴上,点B的坐标为($\frac{2}{3}$,0),先将抛物线C1绕点O顺时针旋转180°得到抛物线C2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任意三角形的内角和都是180° | |
| B. | 三角形按边分可分为不等边三角形和等腰三角形 | |
| C. | 三角形的中线、角平分线、高都是线段 | |
| D. | 三角形的一个外角大于任何一个内角 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
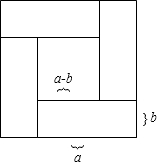 用四个相同的长方形与一个小正方形无重叠、无缝隙地拼成一个大正方形的图案(如图),则由图形能得出(a-b)2=(a+b)2-4ab(化为a、b两数和与积的形式)
用四个相同的长方形与一个小正方形无重叠、无缝隙地拼成一个大正方形的图案(如图),则由图形能得出(a-b)2=(a+b)2-4ab(化为a、b两数和与积的形式)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com