
 ��ͼ���ھ���ABCD�У�AD=3��AB=6��EΪCD���е㣬FΪAD��һ�㣬��AFΪ����������AFGH��ʹ������AFGH�;���ABCD��AD��ͬ�࣬��������AFGH�Ķ���Gǡ�����ڶԽ���BD�ϣ���������AFGH��ÿ��һ����λ���ٶ�������AB����ƽ�ƣ���ƽ���е�������AFGHΪ������A��FGH������A�����B�غ�ʱֹͣ�˶������˶���ʱ��Ϊt��t��0����
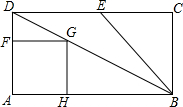
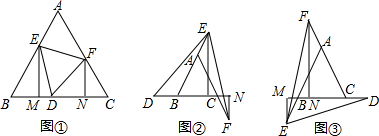
��ͼ���ھ���ABCD�У�AD=3��AB=6��EΪCD���е㣬FΪAD��һ�㣬��AFΪ����������AFGH��ʹ������AFGH�;���ABCD��AD��ͬ�࣬��������AFGH�Ķ���Gǡ�����ڶԽ���BD�ϣ���������AFGH��ÿ��һ����λ���ٶ�������AB����ƽ�ƣ���ƽ���е�������AFGHΪ������A��FGH������A�����B�غ�ʱֹͣ�˶������˶���ʱ��Ϊt��t��0�������� ��1���ɡ�DFG�ס�DAB����$\frac{FG}{AB}=\frac{DF}{AD}$���г����̼��ɽ����
��2�����������Σ���0��t��2ʱ��ͼ1���ɡ�MGN�ס�BAD�����MG��GN���ɽ�����ڵ�2��t��4ʱ��ͼ2������s=S�ı���FGNM-S��PGK���ɽ�����۵�4��t��6ʱ��ͼ3�У�����s=s��BMK�����MK���ɽ����
��3�����ڣ���ͼ4�У��ӳ�HG��CD��N�����á�EMN�ա�MA��H�����MH��HB���ɽ�����⣮
��� �⣺��1�����ı���AFGH�������Σ�
��FG��AB��
���DFG�ס�DAB��
��$\frac{FG}{AB}=\frac{DF}{AD}$��
��������AFGH�ı߳�Ϊx����FG=AF=x��
��DF=AD-AF=3-x��
��$\frac{x}{6}=\frac{3-x}{3}$��
��ã�x=2��
��������AFGH�ı߳�Ϊ2��
��2����ͼ1�У��ӳ�FG��EB��P��FG��BD���ڵ�M��GH��BD���ڵ�N��
��PM��DE��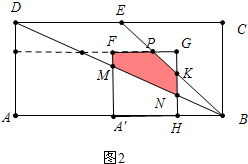
��$\frac{PM}{DE}=\frac{BM}{BD}=\frac{AF}{AD}=\frac{2}{3}$��
��PM=2��
�ٵ�0��t��2ʱ���ߡ�GMN=��ABD����MGN=��DAB=90�㣬
���MGN�ס�BAD��
��$\frac{MG}{AB}=\frac{GN}{AD}$��
��GM=$\frac{1}{2}MG$=$\frac{1}{2}$t��
��s=$\frac{1}{2}$•t•$\frac{1}{2}$t=$\frac{1}{4}$t2��
�ڵ�2��t��4ʱ����ͼ2�У�FM=$\frac{1}{2}$��t-2����
��NH��AD��
��$\frac{NH}{AD}=\frac{BH}{BA}$��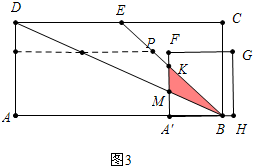
��$\frac{NH}{3}=\frac{4-t}{6}$��
��NH=$\frac{1}{2}��4-t��$��NG=2-NH=$\frac{t}{2}$��
��EC=BC����C=90�㣬
���CEB=��EBC=��HBK=45�㣬
���HKB=��PKG=��KPG=45�㣬
��KH=BH��GK=2-BH=t-2��
��s=S�ı���FGNM-S��PGK=$\frac{1}{2}$[$\frac{1}{2}$��t-2��+$\frac{1}{2}t$]•2-$\frac{1}{2}$��t-2��2=-$\frac{1}{2}$t2+3t-3��
�۵�4��t��6ʱ����ͼ3�У���A��B=A��K=6-t��A��M=$\frac{1}{2}$A��B=$\frac{1}{2}$��6-t����
��s=$\frac{1}{2}$[��6-t��-$\frac{1}{2}$��6-t��]��6-t��=$\frac{1}{4}$��6-t��2��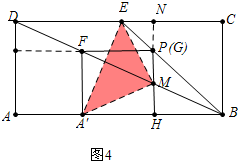
��3�����ڣ���ͼ4�У��ӳ�HG��CD��N��
��CD��BA��NH��AB��
��NH��CD����ENH=90�㣬
��ME=MA�䣬��EMA��=90�㣬
���A��MH+��EMN=90�㣬��EMN+��MEN=90�㣬
���A��MH=��MEN��
�ڡ�A��HM�͡�MNE�У�
$\left\{\begin{array}{l}{��ENM=��A��HM}\\{��MEN=��A��MH}\\{EM=A��M}\end{array}\right.$��
���EMN�ա�MA��H��
��MN=A��H=2��HM=HN-MN=1��
��BH=2HM=2��
��t+2+2=6��
��t=2��
��t=2ʱ����A��EMΪ����ֱ�������Σ�
���� ���⿼��ȫ�������ε��ж������ʡ����������ε��ж������ʡ������ε����ʡ����ε����ʵ�֪ʶ������Ĺؼ�����ȷȷ���Ա�����ȡֵ��Χ������ͼ�Σ��ڽ�����Ҫ��������ȫ�������ν�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{3}$ | B�� | $\frac{1}{3}$ | C�� | $��\frac{1}{3}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
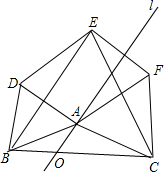 ��ͼ����֪�߶�BC=6��OΪ�߶�BC��һ�㣬��OB=2����O���ֱ��l��BC�ļн���60�㣬AΪl�ϵ�һ�����㣬�ֱ���AC��BCΪ����BC��ͬ�����ȱߡ�ABD����ACF����BCE������EF����ƽ���ı��Σ����Σ����Σ��߶Σ����������з����Ե�A��D��E��F���ɵ�ͼ���У�������
��ͼ����֪�߶�BC=6��OΪ�߶�BC��һ�㣬��OB=2����O���ֱ��l��BC�ļн���60�㣬AΪl�ϵ�һ�����㣬�ֱ���AC��BCΪ����BC��ͬ�����ȱߡ�ABD����ACF����BCE������EF����ƽ���ı��Σ����Σ����Σ��߶Σ����������з����Ե�A��D��E��F���ɵ�ͼ���У�������| A�� | 3�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com