
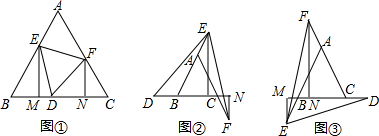
分析 (1)由△BED≌△CDF得到BE=CD,BD=CF,设BE=a,CF=b,则BC=a+b,求出MN与EM+FN(用a的代数式表示)即可证明.
(2)证明方法类似(1),形变证明方法基本不变,
(3)分类讨论在图①求出EM、MD在RT△EMD中利用勾股定理即可,在图②计算方法类似.
解答 (1)证明: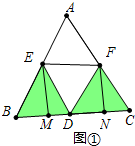 如图①中,∵△ABC是等边三角形,
如图①中,∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵∠DEF=∠A=60°,ED=EF,
∴△DEF是等边三角形,
∴∠EDF=60°,DE=DF,
∵∠EDC=∠B+∠BED=∠EDF+∠FDC,
∴∠BED=∠FDC,
在△BED和△CDF中,
$\left\{\begin{array}{l}{∠B=∠C}\\{∠BED=∠FDC}\\{DE=DF}\end{array}\right.$,
∴△BED≌△CDF,
∴BE=CD,BD=CF,设BE=a,CF=b,则BC=a+b,
∵EM⊥BC,FN⊥BC,∠BEM=∠CFN=30°,
∴BM=$\frac{1}{2}a$,CN=$\frac{1}{2}$b,
∴MN=BC-BM-CN=a+b-$\frac{1}{2}$a-$\frac{1}{2}$b=$\frac{1}{2}$(a+b),EM+FN=$\frac{\sqrt{3}}{2}$a+$\frac{\sqrt{3}}{2}$b=$\frac{1}{2}$(a+b)•$\sqrt{3}$,
∴EM+FN=$\sqrt{3}$MN.
(2)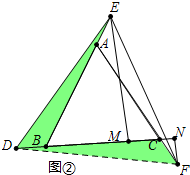 结论EM-FN=$\sqrt{3}$MN.理由如下,
结论EM-FN=$\sqrt{3}$MN.理由如下,
如图②中,连接DF,∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,∠DBE=∠DCE=120°,
∵∠DEF=∠A=60°,ED=EF,
∴△DEF是等边三角形,
∴∠EDF=60°,DE=DF,
∵∠ABC=∠BDE+∠BED=60°,∠EDF=∠FDC+∠BDE,
∴∠BED=∠FDC,
在△BED和△CDF中,
$\left\{\begin{array}{l}{∠DBE=∠DCF}\\{∠BED=∠FDC}\\{DE=DF}\end{array}\right.$,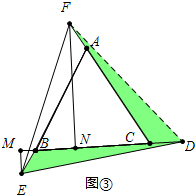
∴△BED≌△CDF,
∴BE=CD,BD=CF,设BE=a,CF=b,则BC=a-b
∵EM⊥BC,FN⊥BC,∠BEM=∠CFN=30°,
∴BM=$\frac{1}{2}a$,CN=$\frac{1}{2}$b,
∴MN=BC-BM+CN=a-b-$\frac{1}{2}$a+$\frac{1}{2}$b=$\frac{1}{2}$(a-b),EM+FN=$\frac{\sqrt{3}}{2}$a-$\frac{\sqrt{3}}{2}$b=$\frac{1}{2}$(a-b)•$\sqrt{3}$,
∴EM-FN=$\sqrt{3}$MN.
如图③中,结论:FN-EM=$\sqrt{3}$MN,(证明方法类似②)
(3)在图①中,∵S△ABC=4$\sqrt{3}$,BE=$\frac{1}{4}$AB,
∴$\frac{\sqrt{3}}{4}$AB2=4$\sqrt{3}$,
∴AB=4,BE=1,由①可知BE+CF=BC,
∴CF=BD=3,EM=$\frac{\sqrt{3}}{2}$,BM=$\frac{1}{2}$,DM=$\frac{5}{2}$,
∴DE=$\sqrt{M{E}^{2}+D{M}^{2}}$=$\sqrt{7}$.
在图②不合题意,在图③中,∵BE=CD=1,BM=$\frac{1}{2}$,EM=$\frac{\sqrt{3}}{2}$,
在RT△DEM中,∵DM=$\frac{13}{2}$,ME=$\frac{\sqrt{3}}{2}$,
∴DE=$\sqrt{D{M}^{2}+M{E}^{2}}$=$\sqrt{43}$,
故答案为$\sqrt{7}$或$\sqrt{43}$.
点评 本题考查全等三角形的判定和性质,等边三角形的性质,解题关键是寻找全等三角形,注意这种形变条件不变的题目在证明过程中方法是类似的,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
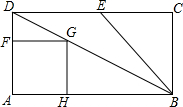 如图,在矩形ABCD中,AD=3,AB=6,E为CD边中点,F为AD上一点,以AF为边作正方形AFGH,使正方形AFGH和矩形ABCD在AD的同侧,且正方形AFGH的顶点G恰好落在对角线BD上,将正方形AFGH以每秒一个单位的速度沿射线AB方向平移,记平行中的正方形AFGH为正方形A′FGH,当点A′与点B重合时停止运动,设运动的时间为t(t≥0).
如图,在矩形ABCD中,AD=3,AB=6,E为CD边中点,F为AD上一点,以AF为边作正方形AFGH,使正方形AFGH和矩形ABCD在AD的同侧,且正方形AFGH的顶点G恰好落在对角线BD上,将正方形AFGH以每秒一个单位的速度沿射线AB方向平移,记平行中的正方形AFGH为正方形A′FGH,当点A′与点B重合时停止运动,设运动的时间为t(t≥0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,且BE=2AE,已知AD=3$\sqrt{3}$,tan∠BCE=$\frac{\sqrt{3}}{3}$,那么CE等于( )
如图所示,在△ABC中,AD⊥BC于D,CE⊥AB于E,且BE=2AE,已知AD=3$\sqrt{3}$,tan∠BCE=$\frac{\sqrt{3}}{3}$,那么CE等于( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$-2 | C. | 5$\sqrt{2}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
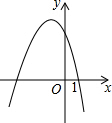 二次函数y=ax2+bx+c的图象如图所示,则化简二次根式$\sqrt{(a+c)^{2}}$+$\sqrt{(b-c)^{2}}$的结果是( )
二次函数y=ax2+bx+c的图象如图所示,则化简二次根式$\sqrt{(a+c)^{2}}$+$\sqrt{(b-c)^{2}}$的结果是( )| A. | a+b | B. | -a-b | C. | 2b-c | D. | -2b+c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
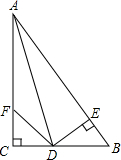 如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上,连接
如图,在△ABC中,∠C=90°,∠CAD=∠BAD,DE⊥AB于E,点F在边AC上,连接查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com