
如图,AB为⊙O的直径,AD为弦,∠DBC=∠A.
(1)求证:BC是⊙O的切线;
(2)连接OC,如果OC恰好经过弦BD的中点E,且tanC=
 ,AD=3,求直径AB的长.
,AD=3,求直径AB的长.


【考点】切线的判定.
【专题】证明题.
【分析】(1)由AB为⊙O的直径,可得∠D=90°,继而可得∠ABD+∠A=90°,又由∠DBC=∠A,即可得∠DBC+∠ABD=90°,则可证得BC是⊙O的切线;
(2)根据点O是AB的中点,点E时BD的中点可知OE是△ABD的中位线,故AD∥OE,则∠A=∠BOC,再由(1)∠D=∠OBC=90°,故∠C=∠ABD,由tanC=
 可知tan∠ABD=
可知tan∠ABD=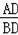
 =
=
 ,由此可得出结论.
,由此可得出结论.
【解答】(1)证明:∵AB为⊙O的直径,
∴∠D=90°,
∴∠ABD+∠A=90°,
∵∠DBC=∠A,
∴∠DBC+∠ABD=90°,即AB⊥BC,
∴BC是⊙O的切线;
(2)∵点O是AB的中点,点E时BD的中点,
∴OE是△ABD的中位线,
∴AD∥OE,
∴∠A=∠BOC.、
∵由(1)∠D=∠OBC=90°,
∴∠C=∠ABD,
∵tanC=
 ,
,
∴tan∠ABD=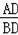
 =
=
 =
=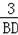
 ,解得BD=6,
,解得BD=6,
∴AB=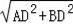
 =
=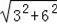
 =3
=3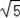
 .
.
【点评】本题考查的是切线的判定,熟知经过半径的外端且垂直于这条半径的直线是圆的切线是解答此题的关键.


科目:初中数学 来源: 题型:
作为宁波市政府民生实事之一的公共自行车建设工作已基本完成,某部门对今年4月份中的7天进行了公共自行车日租车量的统计,结果如图:


(1)求这7天日租车量的众数、中位数和平均数;
(2)用(1)中的平均数估计4月份(30天)共租车多少万车次;
(3)市政府在公共自行车建设项目中共投入9600万元,估计2014年共租车3200万车次,每车次平均收入租车费0.1元,求2014年租车费收入占总投入的百分率(精确到0.1%).
查看答案和解析>>
科目:初中数学 来源: 题型:
九年级某班40位同学的年龄如下表所示:
| 年龄(岁) | 13 | 14 | 15 | 16 |
| 人数 | 3 | 16 | 19 | 2 |
则该班40名同学年龄的众数和中位数分别是( )
A.19,15 B.15,14.5 C.19,14.5 D.15,15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com