练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知数轴上两点A、B对应的数分别为-1、3, 点P是数轴上一动点P

    （1）(4分)若点P到点A,点B的距离相等,求点P对应的数；

    （2） (6分)当点P以每分钟5个单位长度的速度从O点向右运动时,点A以每分钟3个单位长度的速度向右运动,点B以每分钟2个单位长度的速度向右运动,问几分钟时点P到点A,点B的距离相等.

    【答案】（1）1

    （2）分钟或４分钟时点P到点A、点B的距离相等

    【解析】

    （1）解： ∵点P到点A、点B的距离相等,

    ∴点P是线段AB的中点 ……………………………1分

    ∵点A、B对应的数分别为 -1、3,

    ∴点P对应的数是 1 ………………………………….2分

    （2）解: 设分钟时点P到点A、点B的距离相等.

    ∵点A的速度小于点P的速度，

    ∴点A不能超过点P.

    当点p在A、B之间时　　　

    根据题意,得2X+3-5X="5X+1-3X "

    解得X=……………………………………….5分

    　　当点P超过点B时

    5x-（2x+3）=（5x+1）-3x

    　　解得X=4　　　　　…………………………………………９分

    答：分钟或４分钟时点P到点A、点B的距离相等.………………10分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，一架长2.5m的梯子AB斜靠在墙AC上，∠C=90°，此时，梯子的底端B离墙底C的距离BC为0.7m．

    （1）求此时梯子的顶端A距地面的高度AC；

    （2）如果梯子的顶端A下滑了0.9m，那么梯子的顶端B在水平方向上向右滑动了多远？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个正两位数的个位数字是a，十位数字比个位数字大2．

    （1）列式表示这个两位数；

    （2）把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数，试说明新数与原数的和能被22整除．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，对角线AC、BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E．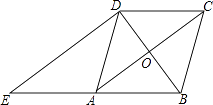
    （1）证明：四边形ACDE是平行四边形；
    （2）若AC=8，BD=6，求△ADE的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A、B在数轴上表示的数分别为m、n．

    （1）对照数轴完成下表：

    （2）若A、B两点间的距离为d，试写出d与m、n之间数量关系，并用文字语言描述

    这个数量关系；

    （3）已知A、B两点在数轴上表示的数分别为x和-2，则A、B两点的距离d可表示

    为 ；如果d=3，求x的值。

    （4）若数轴上表示数m的点位于表示数-5和3的点之间，求|m+5|+|m-3|的值（用含x的式子表示）；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列等式：

    第一个等式：a1==-

    第二个等式：a2==-

    第三个等式：a3==-

    第四个等式：a4==-

    按上述规律，回答下列问题：

    （1）请写出第六个等式：a6=_____=_____；

    （2）用含n的代数式表示第n个等式：an=_____=_____；

    （3）a1+a2+a3+a4+a5+a6=_____（得出最简结果）；

    （4）计算：a1+a2+…+an．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，ABCD的四个顶点的坐标分别为A（0，8），B（﹣6，8），C（﹣6，0），D（0，0），现有动点P在线段CB上运动，当△ADP为等腰三角形时，P点坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形ABCD中，点E、F分别在边CD、AB上，且DE=BF，∠ECA=∠FCA．

    （1）求证：四边形AFCE是菱形；

    （2）若AB=8，BC=4，求菱形AFCE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题情境】

    在△ABC中，AB=AC，点P为BC所在直线上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．当P在BC边上时（如图1），求证：PD+PE=CF．

    图① 图② 图③

    证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．（不要证明）

    【变式探究】

    当点P在CB延长线上时，其余条件不变（如图3）.试探索PD、PE、CF之间的数量关系并说明理由.

    请运用上述解答中所积累的经验和方法完成下列两题：

    【结论运用】

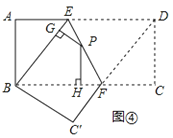
    如图4，将长方形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=8，CF=3，求PG+PH的值；

    【迁移拓展】

    在直角坐标系中.直线l1：y=与直线l2：y=2x+4相交于点A，直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.

    查看答案和解析>>

    同步练习册答案