
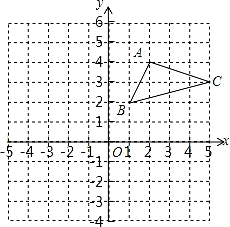
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)写出点A1的坐标;
(3)在x轴上找一点P,使PB+PC的和最小.(标出点P即可,不用求点P的坐标)
科目:初中数学 来源: 题型:
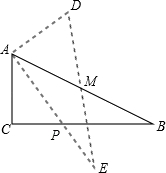
如图,在△ABC中,∠C=90°,AB=10,tanB=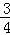 ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
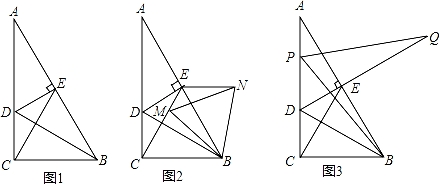
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.
(1)如图1,连接CE,求证:△BCE是等边三角形;
(2)如图2,点M为CE上一点,连结BM,作等边△BMN,连接EN,求证:EN∥BC;
(3)如图3,点P为线段AD上一点,连结BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间 的数量关系,并证明.
的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
如果点M(﹣2,y1),N(﹣1,y2)在抛物线y=﹣x2+2x上,那么下列结论正确的是( )
A.y1<y2 B.y1>y2 C.y1≤y2 D.y1≥y2
查看答案和解析>>
科目:初中数学 来源: 题型:
一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=30cm,点A到地面的距离AD=8cm,旅行箱与水平面AE成60°角,求拉杆把手处C到地面的距离(精确到1cm).(参考数据: )
)
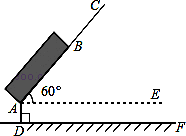
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B.7 C.5 D.4
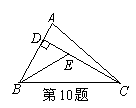
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com