
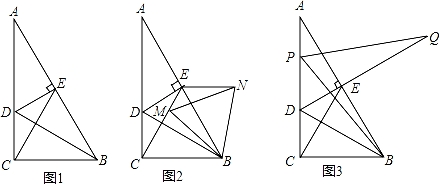
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.
(1)如图1,连接CE,求证:△BCE是等边三角形;
(2)如图2,点M为CE上一点,连结BM,作等边△BMN,连接EN,求证:EN∥BC;
(3)如图3,点P为线段AD上一点,连结BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间 的数量关系,并证明.
的数量关系,并证明.
【考点】全等三角形的判定与性质.
【分析】(1)由直角三角形的性质得出∠ABC=60°,由角平分线的定义得出∠A=∠DBA,证出AD=BD,由线段垂直平分线的性质得出AE=BE,由直角三角形斜边上的中线性质得出CE=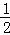 AB=BE,即可得出结论;
AB=BE,即可得出结论;
(2)由等边三角形的性质得出BC=BE,BM=BN,∠EBC=∠MBN=60°,证出∠CBM=∠EBN,由SAS证明△CBM≌△EBN,得出∠BEN=∠BCM=60°,得出∠BEN=∠EBC,即可得出结论;
(3)延长BD至F,使DF=PD,连接PF,证出△PDF为等边三角形,得出PF=PD=DF,∠F=∠PDQ=60°,得到∠F=∠PDQ=60°,证出∠Q=∠PBF,由AAS证明△PFB≌△PDQ,得出DQ=BF=BD+DF=BD+DP,证出AD=BD,即可得出结论.
【解答】(1)证明:∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵BD是△ABC的角平分线,
∴∠DBA=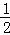 ∠ABC=30°,
∠ABC=30°,
∴∠A=∠DBA,
∴AD=BD,
∵DE⊥AB,
∴AE=BE,
∴CE=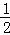 AB=BE,
AB=BE,
∴△BCE是等边三角形;
(2)证明:∵△BCE与△MNB都是等边三角形,
∴BC=BE,BM=BN,∠EBC=∠MBN=60°,
∴∠CBM=∠EBN,
在△CBM和△EBN中,
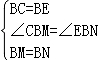 ,
,
∴△CBM≌△EBN(SAS),
∴∠BEN=∠BCM=60°,
∴∠BEN=∠EBC,
∴EN∥BC;
(3)解:DQ=AD+DP;理由如下:
延长BD至F,使DF=PD,连接PF,如图所示:
∵∠PDF=∠BDC=∠A+∠DBA=30°+30°=60°,
∴△PDF为等边三角形,
∴PF=PD=DF,∠F=60°,
∵∠PDQ=90°﹣∠A=60°,
∴∠F=∠PDQ=60°,
∴∠BDQ=180°﹣∠BDC﹣∠PDQ=60°,
∴∠BPQ=∠BDQ=60°,
∴∠Q=∠PBF,
在△PFB和△PDQ中,
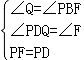 ,
,
∴△PFB≌△PDQ,
∴DQ=BF=BD+DF=BD+DP,
∵∠A=∠ABD,
∴AD=BD,
∴DQ=AD+DP.
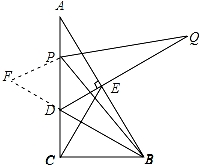
【点评】本题考查了全等三角形的判定与性质、等边三角形的判定与性质、平行线的判定、直角三角形斜边上的中线性质等知识;本题综合性强,有一定难度,特别是(3)中,需要通过作辅助线证明等边三角形和三角形全等才能得出结论.


科目:初中数学 来源: 题型:
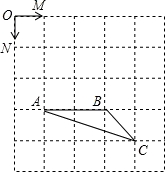
如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点.
(1)记向量 ,
,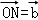 ,试在该网格中作向量
,试在该网格中作向量
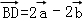 .计算:
.计算: =__________;
=__________;
(2)联结AD,求证:△ABC∽△DAB;
(3)填空:∠ABD=__________度;联结CD,比较∠BDC与∠ACB的大小,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
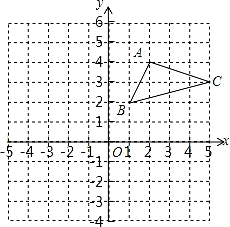
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)写出点A1的坐标;
(3)在x轴上找一点P,使PB+PC的和最小.(标出点P即可,不用求点P的坐标)
查看答案和解析>>
科目:初中数学 来源: 题型:
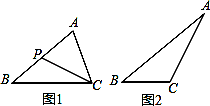
王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题,如图1,在△ABC中,P是边AB上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是 ,或 .
请回答:
(1)王华补充的条件是 ,或 .
(2)请你参考上面的图形和结论,探究,解答下面的问题:
如图2,在△ABC中,∠A=30°,AC2=AB2+AB•BC.求∠C的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com