
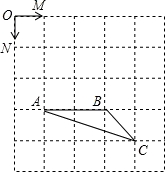
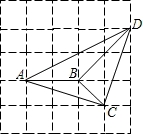
如图,已知正方形网格中每个小正方形的边长为1,点O、M、N、A、B、C都是小正方形的顶点.
(1)记向量 ,
,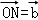 ,试在该网格中作向量
,试在该网格中作向量
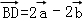 .计算:
.计算: =__________;
=__________;
(2)联结AD,求证:△ABC∽△DAB;
(3)填空:∠ABD=__________度;联结CD,比较∠BDC与∠ACB的大小,并证明你的结论.
【考点】相似形综合题;*平面向量.
【分析】(1)根据平行四 边形法则作向量
边形法则作向量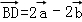 ,小正
,小正 方形的两条对角线的长度即为所求;
方形的两条对角线的长度即为所求;
(2)由图可知△ABC和△DAB各边的长, 根据三角形三边对应成比例证明相似;
根据三角形三边对应成比例证明相似;
(3)由图可知∠ABD=90°+45°=135°,借助于相似三角形(△ABD∽△CBA)的性质来计算.
【解答】(1)解:作向量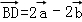 ,
,
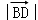 =2
=2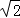 ,
,
故答案为:2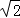 ;
;
(2)证明:∵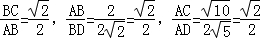 ,
,
∴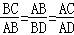 ,
,
∴△ABC∽△DAB;
(3)解:由图可知∠ABD=90°+45°=135°,
故答案为:135°;
∵AC=CD=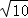 ,
,
∴∠CAD=∠CDA,
又△ABD∽△CBA,
∴∠ADB=∠CAB,
∴∠CAD﹣∠CAB=∠CDA﹣∠ADB,
即∠BAD=∠BDC,
∵∠BAD=∠BCA,
∴∠BDC=∠ACB.
【点评】本题主要考查了平面向量、相似三角形的判定与性质,根据正方形网格中每个小正方形的边长为1,算出各线段的长度是解答此题的关键.


科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交劣弧CB于D,连接AC.
(1)请写出两个不同的正确结论;
(2)若CB=8,ED=2,求⊙O的半径.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
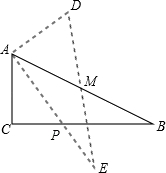
如图,在△ABC中,∠C=90°,AB=10,tanB=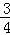 ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
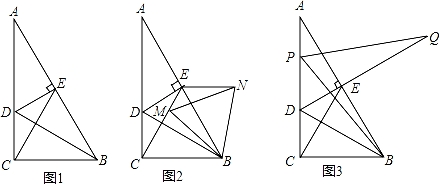
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于E.
(1)如图1,连接CE,求证:△BCE是等边三角形;
(2)如图2,点M为CE上一点,连结BM,作等边△BMN,连接EN,求证:EN∥BC;
(3)如图3,点P为线段AD上一点,连结BP,作∠BPQ=60°,PQ交DE延长线于Q,探究线段PD,DQ与AD之间 的数量关系,并证明.
的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com