
 如图,⊙O的直径为8cm,∠B=30°,∠ACB的平分线交⊙O于D,连接AD.
如图,⊙O的直径为8cm,∠B=30°,∠ACB的平分线交⊙O于D,连接AD.分析 (1)由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠ACB=90°,又由⊙O的直径为8cm,∠B=30°,即可求得答案;
(2)首先连接OD,由CD是∠ACB的角平分线,可求得∠BAD的度数,继而求得答案.
解答 解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=8cm,∠B=30°,
∴AC=$\frac{1}{2}$AB=4cm,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=4$\sqrt{3}$cm;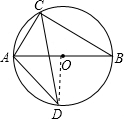 (2)连接OD,
(2)连接OD,
∵CD是∠ACB的角平分线,
∴$\widehat{AD}$=$\widehat{BD}$,
∴∠BOD=$\frac{1}{2}$∠AOB=90°,
∴∠BAD=$\frac{1}{2}$∠BOD=45°,
∵∠BAC=90°-∠B=60°,
∴∠CAD=∠BAC+∠BAD=105°.
点评 此题考查了圆周角定理以及含30°角的直角三角形的性质.注意准确作出辅助线是解此题的关键.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:选择题
 如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2016次操作后得到的折痕D2015E2015到BC的距离记为h2016,到BC的距离记为h2016.若h1=1,则h2016的值为( )
如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1处,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2;按上述方法不断操作下去…,经过第2016次操作后得到的折痕D2015E2015到BC的距离记为h2016,到BC的距离记为h2016.若h1=1,则h2016的值为( )| A. | $\frac{1}{{2}^{2016}}$ | B. | 1-$\frac{1}{{2}^{2016}}$ | C. | $\frac{1}{{2}^{2015}}$ | D. | 2-$\frac{1}{{2}^{2015}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平面直角坐标系xOy中,对于点P(a,b),若点P′的坐标为(a$+\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
平面直角坐标系xOy中,对于点P(a,b),若点P′的坐标为(a$+\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”. 查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=90°,则∠ABC的大小是( )
如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=90°,则∠ABC的大小是( )| A. | 30° | B. | 45° | C. | 60° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
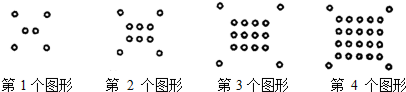
| A. | 4n+(n+1) | B. | n2+4n | C. | 4+n(n+1) | D. | 4+(n+1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com