
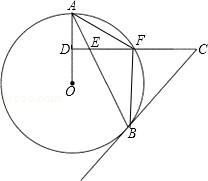
 如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.连结AF、BF.
如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.连结AF、BF.| 5 |
| 13 |
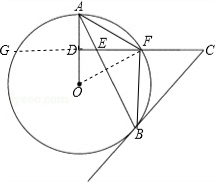 解:(1)如图,连接OF;
解:(1)如图,连接OF;| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| DE |
| AE |
| 5 |
| 13 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 130 |
| 407 |
| 3120 |
| 407 |


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
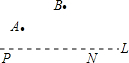 某市计划在一条公路L上修建一个火车站P和一个汽车站N,且使两站相距2km,在公路的一侧有景点A,B.如图所示旅客从P站坐车到两处游玩后,直接到N站坐汽车回到P站,则当P站修在公路何处时,能使旅客所走路程最短?
某市计划在一条公路L上修建一个火车站P和一个汽车站N,且使两站相距2km,在公路的一侧有景点A,B.如图所示旅客从P站坐车到两处游玩后,直接到N站坐汽车回到P站,则当P站修在公路何处时,能使旅客所走路程最短?查看答案和解析>>
科目:初中数学 来源: 题型:
| A、点P与O(0.0)重合 |
| B、连接AB交y轴于P,点P即为所求. |
| C、过点A作x轴的垂线,垂足为P,点P即为所求 |
| D、作点B关于x轴的对称点C,连接AC,交x轴于P,点P即为所求 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
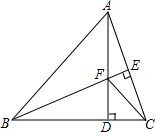 如图△ABC中,AB=BC,BC⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE相交于点F,连接CF.
如图△ABC中,AB=BC,BC⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE相交于点F,连接CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com