
����Ŀ��2019������ڹ���֪������ָ�ϡ��¶���������������ε�������һ������2020��1�£�����ʡ������ҹ���5A�����ξ������ֱ�ΪA�����������ᄚ����B��ƽ�����ɽ�羰��ʤ����C����ˮ���ɽ������D���ػ���ɳ����Ȫ������E����Ҵ�߲���ϼ�������ŷ�ͬѧ�븸ĸ�ƻ�������ڼ����ѡ�־������森
��1���ŷ�һ��ѡ��E����Ҵ�߲ʵ�ϼ�����ĸ����Ƕ��٣�
��2�����ŷ�һ��ѡ����E����Ҵ�߲ʵ�ϼ�����������ٴ�![]() ��
��![]() ��
��![]() ��
��![]() �ĸ���������ѡ��������ȥ���Σ���ѡ
�ĸ���������ѡ��������ȥ���Σ���ѡ![]() ��
��![]() ���������ĸ��ʣ�Ҫ����״ͼ���б�����ʣ���
���������ĸ��ʣ�Ҫ����״ͼ���б�����ʣ���
���𰸡�(1) ![]() ��(2)
��(2) ![]()
��������
(1) �ŷ�һ�ҹ���5�ֿ��ܵ�ѡ��ʽ���ɴ˼��ɳ�ѡ����E�ĸ���Ϊ![]() ��
��
(2) ����״ͼչʾ����12�ֵȿ��ܵĽ�������ҳ�ѡ��A��D���������Ľ������Ȼ����ݸ��ʹ�ʽ���㣮
�⣺(1)�������֪���ŷ�һ�ҹ���5�ֿ��ܵ�ѡ��ʽ��
��ѡ����Ҵ�߲ʵ�ϼ�����ĸ���Ϊ![]() ��
��
�ʴ�Ϊ![]() ��
��
(2)������֪��������״ͼ���£�

����12�ֵȿ��ܵĽ����������ѡ��A��C���������Ľ����Ϊ2��
������ѡ��A��C���������ĸ���=![]() ��
��
�ʴ�Ϊ��![]() ��
��


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2018��12�³���ʼ��ij�ػ�����������һ���![]() ���еĿ����������м�⣬��
���еĿ����������м�⣬��![]() ��Ŀ�����Ⱦָ��(��ƣ�API)��ƽ��ֵ��Ϊÿ���µĿ�����Ⱦָ����
��Ŀ�����Ⱦָ��(��ƣ�API)��ƽ��ֵ��Ϊÿ���µĿ�����Ⱦָ����![]() ���µĿ�����Ⱦָ�����£�
���µĿ�����Ⱦָ�����£�
![]()
![]()
�������������ݣ�
��������
��������������������п�����Ⱦָ�������ݣ�
���� | ��������Ϊ�� | ��������Ϊ�� | ��������Ϊ����Ⱦ |
|
|
|
|
|
˵����������Ⱦָ��![]() ʱ����������Ϊ�ţ�
ʱ����������Ϊ�ţ�![]() ������Ⱦָ��
������Ⱦָ��![]() ʱ����������Ϊ����
ʱ����������Ϊ����![]() ������Ⱦָ��
������Ⱦָ��![]() ʱ����������Ϊ����Ⱦ��
ʱ����������Ϊ����Ⱦ��
�������ݣ�
���еĿ�����Ⱦָ����ƽ��������λ�����������±���ʾ��
���� | ƽ���� | ��λ�� | ���� |
|
|
| |
|
|
|
�뽫������������������
�ó����ۣ������ƶϳ� ����һ���л���״���ȽϺã�����_____��(���ٴ�������ͬ�ĽǶ�˵���ƶϵĺ�����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2020�ڶ��������Ӧ������֪ʶ�������ı�������һ���齱��������ǣ���3�Ŵ�Сһ����������ȫ��ͬ�Ŀ�Ƭ��3�ſ�Ƭ��������д���ݷֱ��ǡ�����֪ʶ�ֲᡷ���Ǻ������Ǻ����������DZ��泯��ϴ�Ⱥ�������һ�ţ��鵽��Ƭ����������ȡ��Ƭ����Ӧ���鼮��
��1��������Ļ�У��������������һ�ſ�Ƭ���������ݺŻأ���������һ�ſ�Ƭ�������б�����״ͼ�ķ�������ǡ�ó鵽2�ſ�Ƭ���ǡ��Ǻ����ĸ��ʣ�
��2�������Ӽ��ź�ԭ��һ���ġ�����֪ʶ�ֲᡷ��Ƭ�������п�Ƭ���泯��ϴ�Ⱥ�������һ�ţ�ʹ�ó鵽������֪ʶ�ֲᡷ��Ƭ�ĸ���Ϊ![]() ����ôӦ���Ӷ����š�����֪ʶ�ֲᡷ��Ƭ����˵�����ɣ�
����ôӦ���Ӷ����š�����֪ʶ�ֲᡷ��Ƭ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻѧ���ǵĿ������ѧУ����չ�ڶ����ã�������γ̿ɹ�ѡ�ֱ��ǡ�A���黭�ࡢB�������ࡢC�����ʵ���ࡢD�������ࡱ���������ȡ�����꼶����ѧ���Ա���������е��飬�����ݵ�����������������������ͳ��ͼ���������ͼ����Ϣ�ش��������⣺
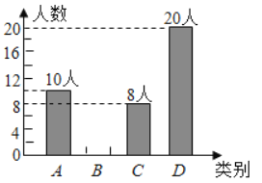
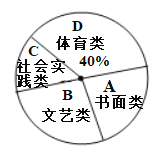
��1�����α�����ѧ������_____________��������ͳ��ͼ�С�A���黭�ࡱ��ռ���ε�Բ�ĽǵĶ���Ϊ___________�ȣ�
��2�����㽫����ͳ��ͼ��ȫ��
��3������У���꼶����600��ѧ����������������������Ƹ�Уѧ��ѡ��C�����ʵ���ࡱ��ѧ�����ж�������
��4�����ε����г������ߣ�1����������Сӱ����ѧ���������б�������״ͼ��������ѡ��ͬһ����Ŀ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
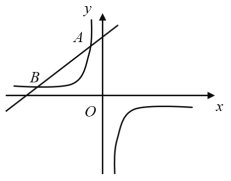
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��
��![]() ������
Ϊ������![]() ����ͼ���ཻ��
����ͼ���ཻ��![]() ��
��![]() ���㣮
���㣮
��1�����������ı���ʽ��
��2����һ�κ���![]() ��ͼ����
��ͼ����![]() ������ƽ��
������ƽ��![]() ����λ
����λ![]() ��ʹƽ�ƺ��ͼ���뷴��������
��ʹƽ�ƺ��ͼ���뷴��������![]() ��ͼ������ֻ��һ�����㣬��
��ͼ������ֻ��һ�����㣬��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�![]() �ڵ�һ���ޣ���
�ڵ�һ���ޣ���![]() �ᣮֱ��
�ᣮֱ��![]() ��ԭ��
��ԭ��![]() ������
������![]() ��������ƽ�ƣ���ƽ�ƹ����У�ֱ�߱�
��������ƽ�ƣ���ƽ�ƹ����У�ֱ�߱�![]() �صõ��߶γ���
�صõ��߶γ���![]() ��ֱ����
��ֱ����![]() ����ƽ�Ƶľ���
����ƽ�Ƶľ���![]() �ĺ���ͼ����ͼ2��ʾ����ô
�ĺ���ͼ����ͼ2��ʾ����ô![]() �����Ϊ�� ��
������� ��
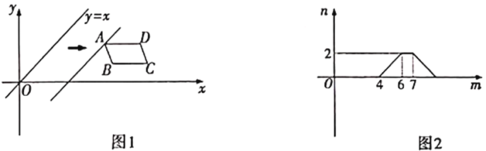
A.3B.![]() C.6D.
C.6D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ƺ����л����������������Ϊĸ�ӣ��ƺӺ����ٲ�λ����ʡ���س���45ǧ�״����ǻƺ���������Ƶ���Ȼ���ۣ������Լ30�ף���ƽ������1010������/�룮����Сʱ��ʱ�䵥λ��������ƽ���������ÿ�ѧ��������ʾΪ��������

A. 6.06��104������/ʱ B. 3.136��106������/ʱ
C. 3.636��106������/ʱ D. 36.36��105������/ʱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ֱ֪��AB�ĺ�������ʽΪy=��2x+8����x�ύ�ڵ�A����y�ύ�ڵ�B��
��1����A��B��������ꣻ
��2������P��m��n��Ϊ�߶�AB�ϵ�һ�����㣨��A��B���غϣ�����PE��x���ڵ�E��PF��y���ڵ�F������EF���ʣ�
������PAO�����ΪS����S����m�ĺ�����ϵʽ����д��m��ȡֵ��Χ��
���Ƿ���ڵ�P��ʹEF��ֵ��С�������ڣ����EF����Сֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧϰ�������ó߹���ͼƽ��һ������ǣ��������ó߹���ͼ���ȷ�һ���������������ѧʷ��һ�����⣬֮����ѧ��֤���Dz�������ɵģ����Ǹ���ʵ����Ҫ��������һ�ּ��ײ�������--------���ֽ�����ͼ1������ʾ��ͼ������![]() ���Բ
���Բ![]() ��ֱ��
��ֱ��![]() ��ͬһֱ�� �ϣ���
��ͬһֱ�� �ϣ���![]() �ij������Բ�İ뾶��ȣ�
�ij������Բ�İ뾶��ȣ�![]() ��
��![]() ��ֱ�ڵ�
��ֱ�ڵ� ![]() �㹻����
�㹻����
ʹ�÷�����ͼ2��ʾ����Ҫ��![]() ���ȷ֣�ֻ���ʵ��������ֽ�����ʹ
���ȷ֣�ֻ���ʵ��������ֽ�����ʹ![]() ����
����![]() �Ķ���
�Ķ���![]() ����
����![]() ���ڱ�
���ڱ�![]() �ϣ���Բ
�ϣ���Բ![]() ����һ��
����һ��![]() ǡ�����У��е�Ϊ
ǡ�����У��е�Ϊ![]() ����
����![]() �Ͱ�
�Ͱ�![]() ���ȷ��ˣ�
���ȷ��ˣ�
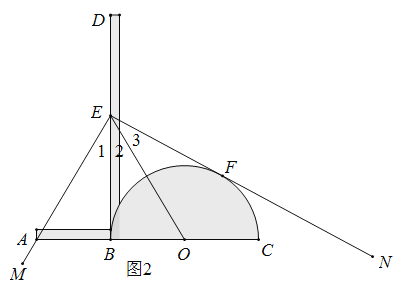
Ϊ��˵����һ��������ȷ�ԣ���Ҫ�������֤�������¸����˲�����������֪��������֤�����벹����������д����֤�������̣�
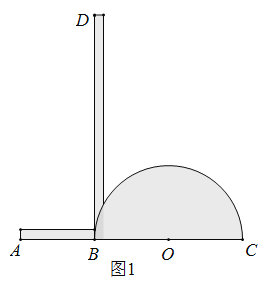
��֪����ͼ2������![]() ͬһֱ���ϣ�
ͬһֱ���ϣ�![]() ����Ϊ��
������![]() ��
��
��֤��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com