
【题目】如图,在△ABC中,点D、E、F分别是边AB、BC、CA上的中点,且AB=6cm,AC=8cm,则四边形ADEF的周长等于cm.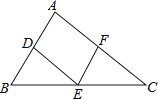
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:
千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:

回答下列问题:
(1)这![]() 筐白菜中,最接近
筐白菜中,最接近![]() 千克的那筐白菜为 千克;
千克的那筐白菜为 千克;
(2)若白菜每千克售价![]() 元,则出售这8筐白菜可卖多少元?
元,则出售这8筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市劲威乡A、B两村盛产柑橘,A村有柑橘200吨,B村有柑橘300吨,现将这些柑橘运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C、D两处的费用分别为每吨15元和18元.设从A村运往C仓库的柑橘重量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元和yB元.
【1】请填写下表

【2】求出yA、yB与x之间的函数解析式;
【3】试讨论A、B两村中,哪个村的运费最少;
【4】考虑B村的经济承受能力,B村的柑橘运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.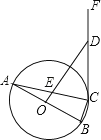
(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为5,BC= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点逆时针旋转度得到的,B1的坐标是;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE是线段AB的延长线,且∠CBE=∠A=∠C.
(1)由∠CBE=∠A可以判断____∥_____,根据是_____________;
(2)由∠CBE=∠C可以判断____∥_____,根据是_____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com