
【题目】如图,已知F是以AC为直径的半圆O上任意一点,过AC上任意一点H作AC的垂线分别交CF,AF的延长线于点E,B,点D是线段BE的中点.
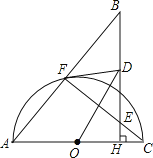
(1)求证:DF是⊙O的切线;
(2)若BF=AF,求证AF2=EF·CF.
【答案】(1)证明见解析;(2)证明见解析.
【解析】分析:(1)连接OF,根据圆周角定理得出∠AFC=90°,然后根据直角三角形斜边中线的性质求得DF=DE=![]() BE,根据等边对等角得出∠1=∠2,∠3=∠C,进而求得OF⊥DF,即可证得DF是 O的切线.(2)由∠C=∠BEF,∠EFB=∠AFC,可推出△EFB∽△AFC,进而推出
BE,根据等边对等角得出∠1=∠2,∠3=∠C,进而求得OF⊥DF,即可证得DF是 O的切线.(2)由∠C=∠BEF,∠EFB=∠AFC,可推出△EFB∽△AFC,进而推出![]() ,即可求解.
,即可求解.
本题解析:1)证明:如图1,连接OF,
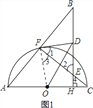
∵AC是直径∴∠AFC=90°∴∠BFE=90°,
∵D是BE的中点∴DF=DE=![]() BE,∴∠1=∠2,
BE,∴∠1=∠2,
∵OF=OC,∴∠3=∠C,∴∠1+∠3=∠2+∠C=∠4+∠C,
∵BH⊥AC,∴在Rt△ECH中,∠4+∠C=90°,
∴∠1+∠3=90°,∴∠DFO=90°,∴OF⊥DF,
∴DF是O的切线。
(2)∵∠C=∠BEF,∠EFB=∠AFC, ∴△EFB∽△AFC,∴![]() ,即AF·BF= EF·CF,又BF=AF,∴AF2=EF·CF.
,即AF·BF= EF·CF,又BF=AF,∴AF2=EF·CF.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中: ①AH=DF;
②∠AEF=45°;
③S四边形EFHG=S△DEF+S△AGH ,
其中正确的结论有 . (填正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC,交直线m于点E,垂足为点F,连接CD,BE.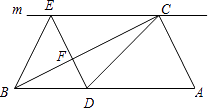
(1)求证:CE=AD;
(2)当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)当∠A的大小满足什么条件时,四边形BECD是正方形?(不需要证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C.其中正确的有( )
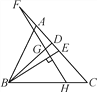
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com