
分析 (1)因为点P的纵坐标是非负数,由此可确定点P的位置.
(2)求出d1与d2即可判定.
(3)分两种情形讨论::①当点Q在x轴上时,点Q坐标为(m,0).由题意可知:$\frac{1}{2}$($\frac{1}{4}{m}^{2}$+1)=2,解方程即可.②当点Q在y轴上点P的下方时,由题意可知:$\frac{1}{4}$m2+1=2[2-($\frac{1}{4}$m2+1],解方程即可,当点Q在y轴上点P的上方时,由题意可知:$\frac{1}{4}$m2+1=2[($\frac{1}{4}$m2+1)-2],解方程即可.
解答 (1)解:∵点P的坐标为(m,$\frac{1}{4}$m2+1),
又∵$\frac{1}{4}$m2+1>0,
∴点P在x轴的上方.
故答案为x轴的上方.
(2)证明:∵P的坐标为(m,$\frac{1}{4}$m2+1);
∴d1=$\frac{1}{4}$m2+1,
P到点F(0,2)的距离为d2=$\sqrt{{m}^{2}+(\frac{1}{4}{m}^{2}-1)^{2}}$=$\sqrt{\frac{1}{16}{m}^{4}+\frac{1}{2}{m}^{2}+1}$=$\sqrt{(\frac{1}{4}{m}^{2}+1)^{2}}$=$\frac{1}{4}{m}^{2}+1$
∴d1=d2.
(3)解:①当点Q在x轴上时,点Q坐标为(m,0).
由题意可知:$\frac{1}{2}$($\frac{1}{4}{m}^{2}$+1)=2,解得m=$±2\sqrt{3}$,
∴点Q(2$\sqrt{3}$,0)或(-2$\sqrt{3}$,0).
②当点Q在y轴上点P的下方时,由题意:$\frac{1}{4}$m2+1=2[2-($\frac{1}{4}$m2+1],解得m=$±\frac{2\sqrt{3}}{3}$,此时点Q(0,$\frac{4}{3}$),
当点Q在y轴上点P的上方时,由题意:$\frac{1}{4}$m2+1=2[($\frac{1}{4}$m2+1)-2],解得m=$±2\sqrt{3}$,此时点Q(0,6),
综上所述点Q的坐标为(2$\sqrt{3}$,0)或(-2$\sqrt{3}$,0)或(0,$\frac{4}{3}$)和(0,6).
点评 本题考查坐标与图形的性质、等边三角形的性质,两点间的距离公式等知识,学会分类讨论的方法,用方程的思想去思考问题,本题易漏解.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
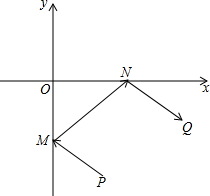 牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.
牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
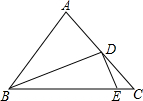 如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD,垂足为D,DE交BC于点E.若DE=5,BD=12,则CD的长为( )
如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD,垂足为D,DE交BC于点E.若DE=5,BD=12,则CD的长为( )| A. | 6 | B. | 6.5 | C. | 7 | D. | 7.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )
如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.AB=10,CD=6.则四边形DMNC的面积( )| A. | 等于24 | B. | 最小为24 | C. | 等于48 | D. | 最大为48 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
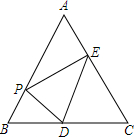 如图,在等边三角形ABC中,AB=6,点P是AB边上的任意一点(点P不与点A、点B重合),过点P作PD⊥AB,交直线BC于点D,作PE⊥AC,垂足为点F.
如图,在等边三角形ABC中,AB=6,点P是AB边上的任意一点(点P不与点A、点B重合),过点P作PD⊥AB,交直线BC于点D,作PE⊥AC,垂足为点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
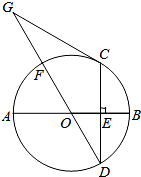 如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°
如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com