
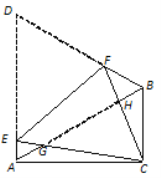
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°, △ABD是等边三角形,将四边形ACBD沿直线EF折叠,使D与C重合,CE与CF分别交AB于点G、H.
(1)求证:△AEG∽△CHG;
(2)△AEG与△BHF是否相似,并说明理由;
(3)若BC=1,求cos∠CHG的值.
【答案】(1)证明见解析(2)△AEG与△BHF相似 (3)![]()
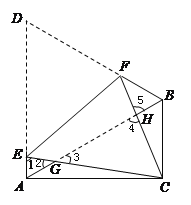
【解析】试题分析:(1)由于△ABD是等边三角形,那么∠D=∠EAG=60°,根据折叠的性质知:∠D=∠GCH=∠AEG=60°,再加上对顶角∠EGA=∠HGC,即可证得所求的三角形相似;
(2)由△ABD是等边三角形和的性质知:∠BAD=∠GCH=∠ABD,再由三角形内角和定理可证明∠1=∠5,即可得到结论;
(3)在Rt△ABC中,已知了BC的长和∠BAC的度数,即可求得AB、AC的值,由折叠的性质知:DE=CE,可设出DE、CE的长,然后表示出AE的长,进而可在Rt△AEC中,由勾股定理求得AE、CE的值,即可得到∠AEG的余弦值,而根据(1)的相似三角形知∠AEG=∠CHG,由此得解.
试题解析:解:(1)∵△ABD是等边三角形,∴∠EAG=∠D=60°;
根据折叠的性质知:DE=CE,∠D=∠GCH=∠EAG=60°,又∵∠EGA=∠HGC,∴△AEG∽△CHG.
(2)△AEG与△BHF相似.理由如下:
∵∠BAD=∠ABD=∠D,∠GCH=∠D,∴∠BAD=∠GCH=∠ABD,∴∠1+∠2=∠3+∠4.∵∠2=∠3,∠4=∠5,∴∠1=∠5, ∴△AEG∽△BHF;
(3)△ABC中,∠BAC=30°,BC=1,则AC=![]() ,AB=2,故AD=AB=2.
,AB=2,故AD=AB=2.
设DE=EC=x,则AE=2﹣x.
在Rt△AEC中,由勾股定理,得:(2﹣x)2+3=x2,解得x=![]() ,∴AE=
,∴AE=![]() ,EC=
,EC=![]() ,∴cos∠AEC=
,∴cos∠AEC=![]() =
=![]() .由(1)的相似三角形知:∠AEG=∠CHG,故cos∠CHG=cos∠AEC=
.由(1)的相似三角形知:∠AEG=∠CHG,故cos∠CHG=cos∠AEC=![]() .
.


科目:初中数学 来源: 题型:
【题目】某织布厂有150名工人,为了提高经济效益,增设制衣项目,已知每人每天能织布30m,或利用所织布制衣4件,制衣一件需要布1.5m,将布直接出售,每米布可获利2元,将布制成衣后出售,每件可获利25元,若每名工人每天只能做一项工作,且不计其他因素,设安排x名工人制衣.
(1)一天中制衣所获利润P是多少(用含x的式子表示);
(2)一天中剩余布所获利润Q是多少 (用含x的式子表示);.
(3)一天当中安排多少名工人制衣时,所获利润为11806元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,
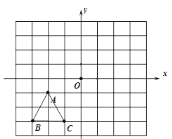
(1)若将△ABC 向右平移三个单位长度得到△A1B1C1,则点 A1 的坐标为________![]()
(2)若△ABC 与△A2B2C2 关于原点 O 成中心对称,则点 A2 的坐标________;
(3)画出△ABC 绕原点 O 顺时针旋转 90°后的对应图形△A3B3C3,并写出 A3 的坐标_____
查看答案和解析>>
科目:初中数学 来源: 题型:
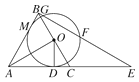
【题目】如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.
(1)求证:AB与⊙O相切;
(2)若AB=4,求线段GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织七年级400名学生参加北京夏令营,已知用3辆小客车和1辆大客车每次可运送学生105人;用1辆小客车和2辆大客车每次可运送学生110人;
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若学校计划租用小客车x辆,大客车y辆,一次送完,且恰好每辆车都坐满;
①请你设计出所有的租车方案;
②若小客车每辆需租金4000元,大客车每辆需租金7600元,请选出最省钱的租车方案,并求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明晚饭后外出散步,遇见同学,交谈一会,返回途中在读报厅看了一会报.下图是根据此情景画出的图象,请你回答下列问题:
(1)小明在距家多远遇见同学的,交谈了多少时间?
(2)读报厅离家多远?
(3)小明在哪一段路程中走得最快,速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70千米![]() 小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点,过了5秒后,测得小汽车所在的B点与车速检测仪A之间的距离为100米.
小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A的正前方60米处的C点,过了5秒后,测得小汽车所在的B点与车速检测仪A之间的距离为100米.
![]() 求BC间的距离;
求BC间的距离;![]() 这辆小汽车超速了吗?请说明理由.
这辆小汽车超速了吗?请说明理由.

【答案】这辆小汽车没有超速.
【解析】
(1)根据勾股定理求出BC的长;
(2)直接求出小汽车的时速,进行比较得出答案.
(1)在Rt△ABC中,AC=60 m,
AB=100 m,且AB为斜边,根据勾股定理,得BC=80 m.
(2)这辆小汽车没有超速.
理由:∵80÷5=16(m/s),
而16 m/s=57.6 km/h,57.6<70,
∴这辆小汽车没有超速.
【点睛】
考查勾股定理的应用,熟练掌握勾股定理是解题的关键.
【题型】解答题
【结束】
19
【题目】已知:如图,线段AC和BD相交于点G,连接AB,CD,E是CD上一点,F是DG上一点,![]() ,且
,且![]() .
.
![]() 求证:
求证:![]() ;
;![]() 若
若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
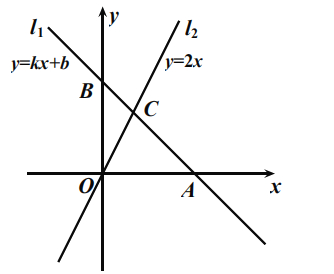
【题目】如图,直线l1:y=kx+b(k≠0)与x轴交于点A(3,O),与y轴交于点B(0,3), 直线l 2:y=2x与直线l1相交于点C.
(1)求直线 l1 的解析式;
(2)求点C的坐标和△AOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com