

分析 过C点作FG⊥AB于F,交DE于G.在Rt△ACF中,根据三角函数可求CF,在Rt△CDG中,根据三角函数可求CG,再根据FG=FC+CG即可求解.
解答 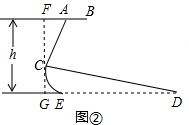 解:过C点作FG⊥AB于F,交DE于G.
解:过C点作FG⊥AB于F,交DE于G.
∵CD与地面DE的夹角∠CDE为12°,∠ACD为80°,
∴∠ACF=∠FCD-∠ACD=∠CGD+∠CDE-∠ACD=90°+12°-80°=22°,
∴∠CAF=68°,
在Rt△ACF中,CF=AC•sin∠CAF≈0.744m,
在Rt△CDG中,CG=CD•sin∠CDE≈0.42m,
∴h=0.42+0.74=1.156≈1.2(米),
答:手柄的一端A离地的高度h约为1.2m.
点评 此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键是用数学知识解决实际问题.


科目:初中数学 来源: 题型:解答题
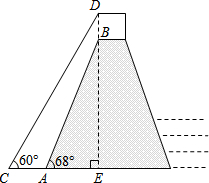 我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到173米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为B,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC.
我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到173米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为B,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,图①是棱长为4cm的立方体,沿其相邻三个面的对角线(虚线)裁掉一个角,得到如图②的几何体,则一只蚂蚁沿着图②几何体的表面,从顶点A爬到顶点B的最短距离为(2$\sqrt{2}$+2$\sqrt{6}$)cm.
如图,图①是棱长为4cm的立方体,沿其相邻三个面的对角线(虚线)裁掉一个角,得到如图②的几何体,则一只蚂蚁沿着图②几何体的表面,从顶点A爬到顶点B的最短距离为(2$\sqrt{2}$+2$\sqrt{6}$)cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com