
【题目】设点A(x1 , y1)和B(x2 , y2)是反比例函数y= ![]() 图象上的两个点,当x1<x2<0时,y1<y2 , 则一次函数y=﹣2x+k的图象不经过的象限是( )
图象上的两个点,当x1<x2<0时,y1<y2 , 则一次函数y=﹣2x+k的图象不经过的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【答案】A
【解析】解:∵点A(x1 , y1)和B(x2 , y2)是反比例函数y= ![]() 图象上的两个点,当x1<x2<0时,y1<y2 ,
图象上的两个点,当x1<x2<0时,y1<y2 ,
∴x1<x2<0时,y随x的增大而增大,
∴k<0,
∴一次函数y=﹣2x+k的图象不经过的象限是:第一象限.
故选:A.
【考点精析】根据题目的已知条件,利用反比例函数的图象和反比例函数的性质的相关知识可以得到问题的答案,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园的门票每张10元,为了吸引更多的游客,该公园管理除保留原来的售票方法外,还推出了一种“购买年卡”的优惠方法,年卡分为A、B、C三种:A卡每张120元,持卡进入不用再买门票;B卡每张60元,持卡进入公园需要再买门票,每张2元;C卡每张30元,持票进入公园时,购买每张4元的门票.
(1)如果你只选择一种购买门票的方式,并且你计划在一年中用100元花在去该公园玩的门票上,请问哪种购票方式可使你进入该公园的次数最多?
(2)求一年中进入该公园至少多少次,购买A类年票比较合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
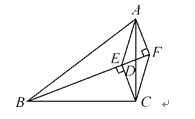
【题目】如图所示,BD是△ABC的中线,CE⊥BD于点E,AF⊥BD,交BD的延长线于点F.
(1)试探索BE,BF和BD三者之间的数量关系,并加以证明;
(2)连接AE,CF,求证:AE∥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( ) 
A.( ![]() ,n)
,n)
B.(m,n)
C.(m, ![]() )
)
D.( ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是x轴上使得|PA﹣PB|的值最大的点,Q是y轴上使得QA+QB的值最小的点,则OPOQ= . 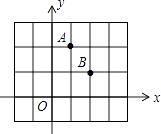
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某晚报“百姓热线”一周内接到热线电话的统计图,其中有关环境保护问题的电话最多,共70个,请回答下列问题:

(1)本周“百姓热线”共接到热线电话多少个?
(2)有关道路交通问题的电话多少个?
(3)计算其他各类电话的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答下列问题.
已知平面内两点 M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算: MN= ![]() .
.
例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ=![]() =
=![]() .
.
特别地,如果两点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
(1)已知 A(1,2)、B(﹣2,﹣3),试求 A、B 两点间的距离;
(2)已知 A、B 在平行于 x 轴的同一条直线上,点 A 的横坐标为 5,点 B 的横坐标为﹣1,
试求 A、B 两 点间的距离;
(3)已知△ABC 的顶点坐标分别为 A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC 的形状 吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com