
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 可以由
可以由![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到(点
得到(点![]() 与点
与点![]() 是对应点,点
是对应点,点![]() 与点
与点![]() 是对应点),连接
是对应点),连接![]() ,则
,则![]() 的度数是________.
的度数是________.

【答案】![]()
【解析】
先根据三角形内角和计算出∠ACB=90°-60°=30°,由于△AB′C由△ABC绕点A顺时针旋转90°得到,根据旋转的性质得到AC′=AC,∠C′AB′=∠CAB=90°,∠AC′B′=30°,则△ACC′为等腰直角三角形,得到∠AC′C=45°,然后利用∠CC′B′=∠AC′C-∠AC′B′计算即可.
解:∵∠BAC=90°,∠B=60°,
∴∠ACB=90°-60°=30°,
∵△AB′C由△ABC绕点A顺时针旋转90°得到,
∴AC′=AC,∠C′AB′=∠CAB=90°,∠AC′B′=30°,
∴△ACC′为等腰直角三角形,
∴∠AC′C=45°,
∴∠CC′B′=∠AC′C-∠AC′B′=45°-30°=15°.
故答案为15°.


科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是反比例函数
是反比例函数![]() 在第一象限图象上一点,点
在第一象限图象上一点,点![]() 的坐标为
的坐标为![]() .
.

![]() 当点
当点![]() 的横坐标逐渐增大时,
的横坐标逐渐增大时,![]() 的面积将如何变化?
的面积将如何变化?
![]() 若
若![]() 与
与![]() 均为直角三角形,其中
均为直角三角形,其中![]() ,求此反比例函数的解析式及点
,求此反比例函数的解析式及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
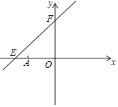
【题目】如图,直线y=kx+6与x轴、y轴分别相交于点E、F,点E的坐标为(-8,0),点A的坐标为(-6,0),点P是直线EF上的一个动点.
(1)求k的值;
(2)点P在第二象限内的直线EF上的运动过程中,写出△OPA的面积S与x的函整表达式,并写出自变量x的取值范围;
(3)探究,当点P在直线EF上运动到时,△OPA的面积可能是15吗,若能,请求出点P的坐标;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种空调共40台.已知购进一台甲种空调比购进一台乙种空调进价多0.2万元;用36万元购进乙种空调数量是用18万元购进甲种空调数量的4倍.请解答下列问题:
(1)求甲、乙两种空调每台进价各是多少万元?
(2)若商场预计投入资金不多于11.5万元用于购买甲、乙两种空调,且购进甲种空调至少14台,商场有哪几种购进方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车的背面,有一种特殊形状的刮雨器,忽略刮雨器的宽度可抽象为一条折线![]() ,如图
,如图![]() 所示,量得连杆
所示,量得连杆![]() 长为
长为![]() ,雨刮杆
,雨刮杆![]() 长为
长为![]() ,
,![]() .若启动一次刮雨器,雨刮杆
.若启动一次刮雨器,雨刮杆![]() 正好扫到水平线
正好扫到水平线![]() 的位置,如图
的位置,如图![]() 所示.
所示.

![]() 求雨刮杆
求雨刮杆![]() 旋转的最大角度及
旋转的最大角度及![]() 、
、![]() 两点之间的距离;
两点之间的距离;
![]() 求雨刮杆
求雨刮杆![]() 扫过的最大面积.
扫过的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一组数9,17,25,33,…,(8n+1)(从左往右数,第1个数是9,第2个数是17,第3个数是25,第4个数是33,依此类推,第n个数是8n+1).设这组数的前n个数的和是sn.
(1)第5个数是多少?并求1892—s5的值;
(2)若n满足方程![]() =
=![]() ,则
,则![]() 的值是整数吗?请说明理由.
的值是整数吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
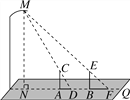
【题目】晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长(结果精确到0.01米).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,分别以△ABC的边AB、AC为一边向形外作正方形ABDE和正方形ACGF.求证S△AEF=S△ABC.
(2)如图②,分别以△ABC的边AB、AC、BC为边向形外作正方形ABDE、ACGF、BCHI,可得六边形DEFGHI,若S正方形ABDE=17,S正方形ACGF=25,S正方形BCHI=16,求S六边形DEFGHI.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com