
 (1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的长度.
(1)如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点,求线段MN的长度.分析 (1)由已知条件可知,MN=MC+NC,又因为点M、N分别是AC、BC的中点,则MC=$\frac{1}{2}$AC,NC=$\frac{1}{2}$BC,故MN=MC+NC=$\frac{1}{2}$(AC+BC),由此即可得出结论;
(2)本题应考虑到A、B、C三点之间的位置关系的多种可能,即当点C在线段AB上时和当点C在线段AB的延长线上时.
解答 解:(1)∵AC=6cm,且M是AC的中点,
∴MC=$\frac{1}{2}$AC=$\frac{1}{2}$6=3cm,
同理:CN=2cm,
∴MN=MC+CN=3cm+2cm=5cm,
∴线段MN的长度是5m;
(2)分两种情况:
当点C在线段AB上,由(1)得MN=5cm,
当C在线段AB的延长线上时,
∵AC=6cm,且M是AC的中点
∴MC=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3cm,
同理:CN=2cm,
∴MN=MC-CN=3cm-2cm=1cm,
∴当C在直线AB上时,线段MN的长度是5cm或1cm.
点评 本题考查了两点间的距离,利用中点性质转化线段之间的倍分关系是解题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F.连接DE,则DF的长是( )
如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F.连接DE,则DF的长是( )| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{7}{8}$ | D. | $\frac{25}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
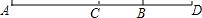 如图,C为线段AD上一点,B为CD的中点,AD=12cm,BD=3cm.
如图,C为线段AD上一点,B为CD的中点,AD=12cm,BD=3cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com