
【题目】如图,△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点A开始沿AC向点C以2厘米/秒的速度运动;与此同时,点Q从点C开始沿CB边向点B以1厘米/秒的速度运动;如果P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动.
(1)经过几秒,△CPQ的面积等于3cm2?
(2)在整个运动过程中,是否存在某一时刻t,使PQ恰好平分△ABC的面积?若存在,求出运动时间t;若不存在,请说明理由.
(3)是否存在某一时刻,PQ长为![]() ,如果存在,求出运动时间t。
,如果存在,求出运动时间t。
【答案】(1)1或3秒;(2)不存在满足条件的t;(3)![]()
【解析】
(1)设出运动所求的时间,可将BP和BQ的长表示出来,代入三角形面积公式,列出等式,可将时间求出;
(2)将△PBQ的面积表示出来,根据△=b2-4ac来判断;
(3)设经过y秒后存在,则PC=8-2y,CQ=y,根据勾股定理可得PC2+CQ2=(![]() )2,求方程即可.
)2,求方程即可.
(1)解:设经过x秒,△CPQ的面积等于3cm2.则
![]() x(8﹣2x)=3,
x(8﹣2x)=3,
化简得x2﹣4x+3=0,
解得x1=1,x2=3;
(2)设存在某一时刻t,使PQ恰好平分△ABC的面积.则
![]() t(8﹣2t)=
t(8﹣2t)=![]() ×
×![]() ×6×8,
×6×8,
化简得t2﹣4t+12=0,
b2﹣4ac=16﹣48=﹣32<0,
故方程无实数根,即不存在满足条件的t.
(3)设经过y秒后存在PQ长为![]() ,则PC=8-2y,CQ=y,
,则PC=8-2y,CQ=y,
∵∠C=90°,
∴PC2+CQ2=(![]() )2,
)2,
解得:y1=![]() ,y2=5(不符合题意,舍去),
,y2=5(不符合题意,舍去),
所以经过![]() 秒后,PQ的长为
秒后,PQ的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】为迎接市教育局开展的“创先争优”主题演讲活动,某校组织党员教师进行演讲预赛.学校将所有参赛教师的成绩(得分为整数,满分为100分)分成四组,绘制了不完整的统计图表如下:
组别 | 成绩x | 组中值 | 频数 |
第一组 | 90≤x≤100 | 95 | 4 |
第二组 | 80≤x<90 | 85 | |
第三组 | 70≤x<80 | 75 | 8 |
第四组 | 60≤x<70 | 65 |
观察图表信息,回答下列问题:
(1)参赛教师共有 人;
(2)如果将各组的组中值视为该组的平均成绩,请你估算所有参赛教师的平均成绩;
(3)成绩落在第一组的恰好是两男两女四位教师,学校从中随机挑选两位教师参加市教育局组织的决赛.通过列表或画树状图求出挑选的两位教师是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )
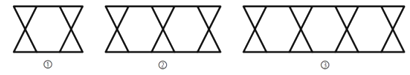
A. 12 B. 14 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有600名学生,在体育中考前进行了一次模拟体测.从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图.请根据相关信息,解答下列问题:
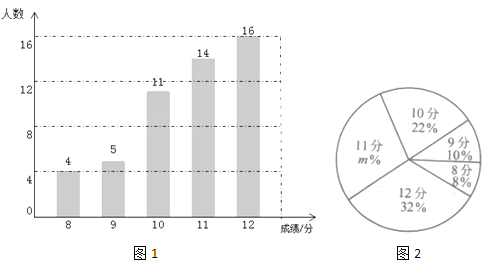
(Ⅰ)本次抽取到的学生人数为 ,图2中![]() 的值为 ;
的值为 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校九年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
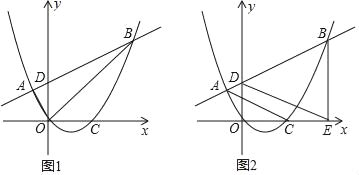
【题目】如图,抛物线y=ax2+bx经过点A(﹣1,![]() )及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
)及原点,交x轴于另一点C(2,0),点D(0,m)是y轴正半轴上一动点,直线AD交抛物线于另一点B.
(1)求抛物线的解析式;
(2)如图1,连接AO、BO,若△OAB的面积为5,求m的值;
(3)如图2,作BE⊥x轴于E,连接AC、DE,当D点运动变化时,AC、DE的位置关系是否变化?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
材料1.若一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
材料2.已知实数m,n满足m2-m-1=0,n2-n-1=0,且m≠n,求![]() 的值.
的值.
解:由题知m,n是方程x2-x-1=0的两个不相等的实数根,
根据材料1得m+n=1,mn=-1,
∴![]() .
.
解决问题:
(1)一元二次方程x2-4x-3=0的两根为x1,x2,则x1+x2= ,x1x2= .
(2)已知实数m,n满足2m2-2m-1=0,2n2-2n-1=0,且m≠n,求m2n+mn2的值.
(3)已知实数p,q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com