
【题目】如图1,已知函数![]() 与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.

(1)求直线BC的函数解析式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.
①若△PQB的面积为![]() ,求点M的坐标;
,求点M的坐标;
②连接BM,如图2,若∠BMP=∠BAC,求点P的坐标.
【答案】(1)![]() ;(2)①M(
;(2)①M(![]() ,0)或(
,0)或(![]() ,0);②P(
,0);②P(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)先根据坐标轴上点的特征求出A、B的坐标,进而求得点C的坐标,最后用待定系数法即可得出结论;
(2) ①设点M的坐标,进而得到点P、Q的坐标,得到PQ长,最后用面积公式即可得出结论;
②利用点C与点A关于y轴对称,QM![]() 轴,证得
轴,证得![]() ;设出M的坐标,利用勾股定理建立方程求解,得到点P的坐标;根据直线BA和BC关于y轴对称,即可求得点P关于y轴对称的另一个点的坐标.
;设出M的坐标,利用勾股定理建立方程求解,得到点P的坐标;根据直线BA和BC关于y轴对称,即可求得点P关于y轴对称的另一个点的坐标.
(1)对于函数![]()
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ;
;
∴直线![]() 与坐标轴的交点坐标为:A(-6,0),B(0,3)
与坐标轴的交点坐标为:A(-6,0),B(0,3)
∵点C与点A关于y轴对称
∴点C的坐标为(6,0)
设直线BC的函数解析式为:![]()
将C (6,0)代入得:![]()
解得:![]()
∴直线BC的函数解析式为:![]()
(2) ①设点M的坐标为(n,0)
∵点P在直线![]() 上,∴点P的坐标为(
上,∴点P的坐标为(![]() ,
,![]() )
)
∵点![]() 在直线
在直线![]() 上,∴点
上,∴点![]() 的坐标为(
的坐标为(![]() ,
,![]() )
)
∴![]()
∵△PQB的面积为![]() ,
,
∴![]()
解得:![]()
∴M(![]() ,0)或(
,0)或(![]() ,0);
,0);
②∵点C与点A关于y轴对称,∴![]() ,
,
∵QM![]() 轴,∴
轴,∴![]() ,
,
∵∠BMP=∠BAC,∴![]() ,
,
∵![]() ,∴
,∴![]()
设点M的坐标为![]() ,则点P的坐标为(
,则点P的坐标为(![]() ,
,![]() )
)
∵![]()
在![]() 中,
中,
![]()
![]()
![]()
∴![]()
∴![]()
解得:![]() ,
,
∴点P的坐标为:(![]() ,
,![]() )
)
∵直线BA和BC关于y轴对称,
∴点P关于y轴的对称点为:(![]() ,
,![]() )
)
故点P的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点是点A(3,0),其部分图象如图,则下列结论:
①2a+b=0;
②b2﹣4ac<0;
③一元二次方程ax2+bx+c=0(a≠0)的另一个解是x=﹣1;
④点(x1,y1),(x2,y2)在抛物线上,若x1<0<x2,则y1<y2.
其中正确的结论是_____(把所有正确结论的序号都填在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
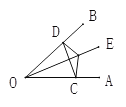
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC 中,AB=AC,点 D 在 AB 边上,点 E 在 AC 的延长线上,且 CE=BD, 连接 DE 交 BC 于点 F.

⑴求证:EF=DF;
⑵如图2,过点 D 作 DG⊥BC,垂足为 G,求证:BC=2FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)若商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么,最多可购买多少件甲种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两名工人各承包了一段500米的道路施工工程,已知甲每天可完成的工程比乙多5米.两人同时开始施工,当乙还有100米没有完成时,甲已经完成全部工程.
(1)求甲、乙每天各可完成多少米道路施工工程?
(2)后来两人又承包了新的道路施工工程,施工速度均不变,乙承包了500米,甲比乙多承包了100米,乙想:这次我们一定能同时完工了!请通过计算说明乙的想法正确吗?若正确,求出两人的施工时间;若不正确,则应该如何调整其中一人的施工速度才能使两人同时完工,请通过计算给出调整方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com