
【题目】甲乙两名工人各承包了一段500米的道路施工工程,已知甲每天可完成的工程比乙多5米.两人同时开始施工,当乙还有100米没有完成时,甲已经完成全部工程.
(1)求甲、乙每天各可完成多少米道路施工工程?
(2)后来两人又承包了新的道路施工工程,施工速度均不变,乙承包了500米,甲比乙多承包了100米,乙想:这次我们一定能同时完工了!请通过计算说明乙的想法正确吗?若正确,求出两人的施工时间;若不正确,则应该如何调整其中一人的施工速度才能使两人同时完工,请通过计算给出调整方案.
【答案】(1)甲每天可完成25米道路施工工程,乙每天可完成20米道路施工工程;(2)不能同时完工,调整方案为:将甲施工速度减少1千米/天或将乙施工速度增加![]() 千米/天,可使两人同时完工.
千米/天,可使两人同时完工.
【解析】
(1)设乙每天施工x米,则甲每天施工(x+5)米,由甲完成500米的时间等于乙完成400米的时间,列出方程可求解;
(2)通过计算即可判断甲乙不能同时完工;分两种方案,然后根据由甲完成600米的时间等于乙完成500米的时间,列出方程可求解.
(1)设乙每天施工x米,则甲每天施工(x+5)米
根据题意可得:![]()
解得:![]()
经检验,![]() 是原方程的解
是原方程的解
则![]() (米)
(米)
答:甲每天可完成25米道路施工工程,乙每天可完成20米道路施工工程;
(2)因为甲完成600米,需要![]() 天,乙完成500米,需要
天,乙完成500米,需要![]() 天
天
所以甲乙不能同时完工,以下两种方案可使得甲乙同时完工:
方案一:将甲施工速度减少a千米/天
根据题意可得:![]()
解得:![]()
经检验,![]() 是原方程的解
是原方程的解
方案二:将乙施工速度增加b千米/天,
根据题意可得:![]()
解得:![]()
经检验,![]() 是原方程的解
是原方程的解
综上,将甲施工速度减少1千米/天或将乙施工速度增加![]() 千米/天,可使两人同时完工.
千米/天,可使两人同时完工.


科目:初中数学 来源: 题型:
【题目】如图1,已知函数![]() 与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.

(1)求直线BC的函数解析式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.
①若△PQB的面积为![]() ,求点M的坐标;
,求点M的坐标;
②连接BM,如图2,若∠BMP=∠BAC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=155°,则∠EDC的度数为( )

A.20°B.20.5°C.21°D.22°
查看答案和解析>>
科目:初中数学 来源: 题型:
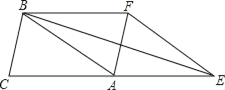
【题目】如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求四边形CEFB的面积;
(2)试判断AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() 。
。
(1)请画出![]() 关于
关于![]() 轴对称后得到的
轴对称后得到的![]() ;
;
(2)直接写出点![]() ,点
,点![]() ,点
,点![]() 的坐标;
的坐标;
(3)在![]() 轴上寻找一个点
轴上寻找一个点![]() ,使
,使![]() 的周长最小,并直接写出
的周长最小,并直接写出![]() 的周长的最小值。
的周长的最小值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国北京已获得2022年第24届冬季奥林匹克运动会举办权,北京也将创造历史,成为第一个既举办过夏奥会又举办冬奥会的城市.张家口也成为本届冬奥会的协办城市,为此,中国设计了第一条采用我国自主研发的北斗卫星导航系统的智能化高速铁路——京张高铁,作为2022年北京冬奥会重要交通保障设施.已知北京至张家口铁路,铁路全长约180千米.按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求高铁列车的平均行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①三点确定一个圆;②平分弦的直径必垂直于这条弦;③圆周角等于圆心角的一半;④等弧所对的圆心角相等;⑤各角相等的圆内接多边形是正多边形.其中正确的有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示.
(1)分别写出下列顶点的坐标:A_______,B______.
(2)顶点A关于y轴对称的点A′的坐标为:A′_______.
(3)△ABC的面积为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com