
【题目】如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=155°,则∠EDC的度数为( )

A.20°B.20.5°C.21°D.22°
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
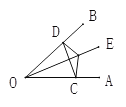
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)若商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么,最多可购买多少件甲种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,请在图中画出△AMN,写出画图过程并直接写出∠MAN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并完成任务:
(1)有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.
例如:![]() 的有理化因式是
的有理化因式是![]() ;
;![]() 的有理化因式是
的有理化因式是![]() .
.
(2)分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去。指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到化去分母中根号的目的.
如: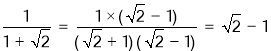 ;
;![]() .
.
知识运用:
(1)填空:![]() 的有理化因式是________________.
的有理化因式是________________.
(2)将下列各式分母有理化:
①![]()
②![]()
③![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
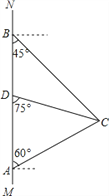
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两名工人各承包了一段500米的道路施工工程,已知甲每天可完成的工程比乙多5米.两人同时开始施工,当乙还有100米没有完成时,甲已经完成全部工程.
(1)求甲、乙每天各可完成多少米道路施工工程?
(2)后来两人又承包了新的道路施工工程,施工速度均不变,乙承包了500米,甲比乙多承包了100米,乙想:这次我们一定能同时完工了!请通过计算说明乙的想法正确吗?若正确,求出两人的施工时间;若不正确,则应该如何调整其中一人的施工速度才能使两人同时完工,请通过计算给出调整方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,四边形![]() 各个顶点坐标分别为
各个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
![]() 画出平面直角坐标系,并画四边形
画出平面直角坐标系,并画四边形![]() .
.
![]() 试确定图中四边形
试确定图中四边形![]() 的面积.
的面积.
![]() 如果将四边形
如果将四边形![]() 绕点
绕点![]() 旋转
旋转![]() ,试确定旋转后四边形上各个顶点的坐标.
,试确定旋转后四边形上各个顶点的坐标.
![]() 如果
如果![]() ,你能重新建立适当的坐标系,横坐标乘以
,你能重新建立适当的坐标系,横坐标乘以![]() 得的图形与原图形重合吗?请说明理由.
得的图形与原图形重合吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com