Question

【题目】如图，直线y=kx+2k（k≠0）与x轴交于点B，与双曲线y=（m+5）x2m+1交于点A、C，其中点A在第一象限，点C在第三象限．

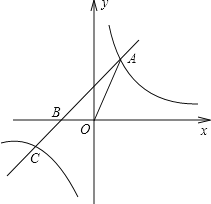
（1）求双曲线的解析式；

（2）求B点的坐标；

（3）若S△AOB=2，求A点的坐标；

（4）在（3）的条件下，在x轴上是否存在点P，使△AOP是等腰三角形？若存在，请直接写出P点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）（2）B（﹣2，0）（3）A（2，2）（4）P1（2，0），P2（4，0），P3（﹣2，0），P4（2，0）

【解析】

试题分析：（1）根据双曲线函数的定义可以确定m的值；

（2）利用y=kx+2k当y=0时，x=2就知道B的坐标；

（3）根据（1）知道OB=2，而S△AOB=2，利用它们可以求出A的坐标；

（4）存在点P，使△AOP是等腰三角形．只是确定P坐标时，题目没有说明谁是腰，是底，所以要分类讨论，不要漏解．

解：（1）∵y=（m+5）x2m+1是双曲线

∴．

∴m=﹣1（2分）

∴（3分）

（2）∵直线y=kx+2k（k≠0）与x轴交于点B

∴当y=0时，0=kx+2k

∴x=﹣2（5分）

∴B（﹣2，0）（6分）

（3）∵B（﹣2，0）

∴OB=2（7分）

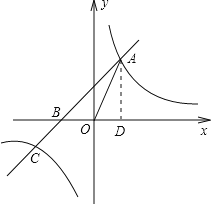
过A作AD⊥x轴于点D

∵点A在双曲线y=上，

∴设A（a，b）

∴ab=4，AD=b（8分）

又∵S△AOB=OBAD=×2b=2

∴b=2（9分）

∴a=2，

∴A（2，2）（10分）

（4）P1（2，0），P2（4，0），P3（﹣2，0），P4（2，0）．

（写对一个得一分）（14分）