
【题目】如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,过点A作⊙O的切线交BC的延长线于点D.
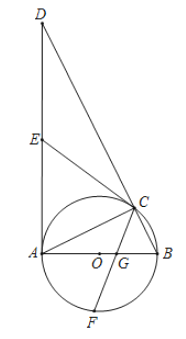
(1)求证:△DAC∽△DBA;
(2)过点C作⊙O的切线CE交AD于点E,求证:CE=![]() AD;
AD;
(3)若点F为直径AB下方半圆的中点,连接CF交AB于点G,且AD=6,AB=3,求CG的长.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)利用AB为⊙O的直径和AD是⊙O的切线,判断出∠ACD=∠BAD=90°,即可得出结论;
(2)利用切线长定理判断出AE=CE,进而得出∠DAC=∠ECA,再用等角的余角相等判断出∠D=∠DCE,得出DE=CE,即可得出结论;
(3)先求出tan∠ABD的值,进而求出GH=2CH,进而得出BC=3BH,再求出BC建立方程求出BH,进而得出GH,即可得出结论.
(1)证明:∵AB是⊙O直径,
∴∠ACD=∠ACB=90°,
∵AD是⊙O的切线,
∴∠BAD=90°,
∴∠ACD=∠BAD=90°,
∵∠D=∠D,
∴△DAC∽△DBA.
(2)证明:∵EA,EC是⊙O的切线,
∴AE=CE,
∴∠DAC=∠ECA,
∵∠ACD=90°,
∴∠ACE+∠DCE=90°,∠DAC+∠D=90°,
∴∠D=∠DCE,
∴DE=CE,
∴AD=AE+DE=CE+CE=2CE,
∴CE=![]() AD.
AD.
(3)解:在Rt△ABD中,AD=6,AB=3,
∴tan∠ABD=![]() =2,
=2,
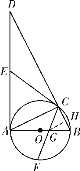
如图,过点G作GH⊥BD于H,
∴tan∠ABD=![]() =2,
=2,
∴GH=2BH,
∵点F是直径AB下方半圆的中点,
∴∠BCF=45°,
∴∠CGH=45°,
∴CH=GH=2BH,
∴BC=BH+CH=3BH,
在Rt△ABC中,tan∠ABC=![]() =2,
=2,
∴AC=2BC,
根据勾股定理得AC2+BC2=AB2,
∴4BC2+BC2=9,
∴BC=![]() ,
,
∴3BH=![]() ,
,
∴BH=![]() ,
,
∴GH=2BH=![]() ,
,
在Rt△CHG中,∠BCF=45°,
∴CG=![]() GH=
GH=![]() .
.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】某县政府计划拨款34000元为福利院购买彩电和冰箱,已知商场彩电标价为2000元/台,冰箱标价为1800元/台,如按标价购买两种家电,恰好将拨款全部用完.
(1)问原计划购买的彩电和冰箱各多少台?
(2)购买的时候恰逢商场正在进行促销活动,全场家电均降价![]() 进行销售,若在不增加县政府实际负担的情况下,能否比原计划多购买3台冰箱?请通过计算回答.
进行销售,若在不增加县政府实际负担的情况下,能否比原计划多购买3台冰箱?请通过计算回答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
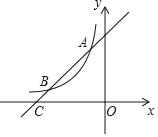
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求a,k的值及点B的坐标;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,直接写出点P的坐标.
S△BOC,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
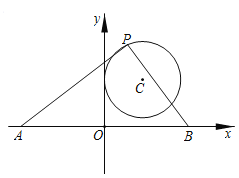
【题目】如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
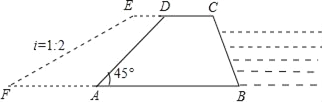
【题目】如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.
(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
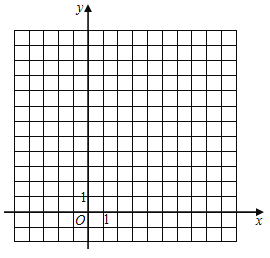
【题目】在平面直角标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4),C(﹣1,6).
(1)画出△ABC,并求出BC所在直线的解析式;
(2)画出△ABC绕点A顺时针旋转90°后得到的△AB1C1,并求出△ABC在上述旋转过程中扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
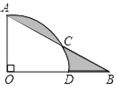
【题目】如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点A、点C,交OB于点D,若OA=3,则阴影都分的面积为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为美化小区环境,物业计划安排甲、乙两个工程队完成小区绿化工作.已知甲工程队每天绿化面积是乙工程队每天绿化面积的2倍,甲工程队单独完成600m2的绿化面积比乙工程队单独完成600m2的绿化面积少用2天.
(1)求甲、乙两工程队每天绿化的面积分别是多少m2;
(2)小区需要绿化的面积为9600m2,物业需付给甲工程队每天绿化费为0.3万元,付给乙工程队每天绿化费为 0.2万元,若要使这次的绿化总费用不超过10万元,则至少应安排甲工程队工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com