
【题目】如图1,矩形![]() 摆放在平面直角坐标系中,点
摆放在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,过点
,过点![]() 的直线交矩形
的直线交矩形![]() 的边
的边![]() 于点
于点![]() ,且点
,且点![]() 不与点
不与点![]() 、
、![]() 重合,过点
重合,过点![]() 作
作![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
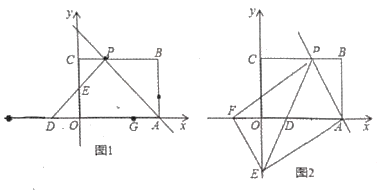
(Ⅰ)若![]() 为等腰直角三角形.
为等腰直角三角形.
①直接写出此时![]() 点的坐标:______;直线
点的坐标:______;直线![]() 的解析式为______;
的解析式为______;
②在![]() 轴上另有一点
轴上另有一点![]() 的坐标为
的坐标为![]() ,请在直线
,请在直线![]() 和
和![]() 轴上分别找一点
轴上分别找一点![]() 、
、![]() ,使
,使![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标和
的坐标和![]() 周长的最小值.
周长的最小值.
(Ⅱ)如图2,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,若以
,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求直线
为顶点的四边形是平行四边形,求直线![]() 的解析式.
的解析式.
科目:初中数学 来源: 题型:
【题目】对于一次函数![]()
![]() ,我们称函数
,我们称函数![]()
![]()
为它的m分函数(其中m为常数).
例如,![]() 的4分函数为:当
的4分函数为:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)如果![]() 的2分函数为
的2分函数为![]() ,
,
① 当![]() 时,
时,![]() ; ②当
; ②当![]() 时,
时,![]() .
.
(2)如果![]() 的-1分函数为
的-1分函数为![]() ,求双曲线
,求双曲线![]() 与
与![]() 的图象的交点坐标;
的图象的交点坐标;
(3)从下面两问中任选一问作答:
①设y=x+2的m分函数为y![]() ,如果抛物线y=x
,如果抛物线y=x![]() 与y
与y![]() 的图象有且只有一个公共点,直接写出m的取值范围。
的图象有且只有一个公共点,直接写出m的取值范围。
②如果点A(0,t)到y=x+2的0分函数y[0]的图象的距离小于1,直接写出t的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将正方形ABCD置于平面直角坐标系中,其中AD边在x轴上,其余各边均与坐标轴平行,直线l:y=x﹣3沿x轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为( )
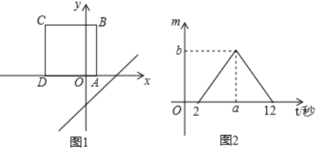
A. 5![]() B. 4
B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义运算:对于任意有理数a、b,都有a![]() b=ab-b,如:2
b=ab-b,如:2![]() 3=2×3-3,请根据以上定义解答下列各题:
3=2×3-3,请根据以上定义解答下列各题:
(1) 2![]() (-3)=___________,x
(-3)=___________,x![]() (-2)=___________;
(-2)=___________;
(2) 化简:[(-x)![]() 3]
3] ![]() (-2);
(-2);
(3) 若x![]()
![]() =3
=3![]() (-x),求x的值.
(-x),求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有![]() 、
、![]() 两个点对应的数分别是
两个点对应的数分别是![]() 、
、![]() ,且满足
,且满足![]() ;
;
![]()
(1)求![]() 、
、![]() 的值;
的值;
(2)点![]() 是数轴上
是数轴上![]() 、
、![]() 之间的一个点,使得
之间的一个点,使得![]() ,求出点
,求出点![]() 所对应的数;
所对应的数;
(3)点![]() ,点
,点![]() 为数轴上的两个动点,点
为数轴上的两个动点,点![]() 从
从![]() 点以3个单位长度每秒的速度向右运动,点
点以3个单位长度每秒的速度向右运动,点![]() 同时从
同时从![]() 点以2个单位长度每秒的速度向左运动,设运动时间为
点以2个单位长度每秒的速度向左运动,设运动时间为![]() 秒,若
秒,若![]() ,求时间
,求时间![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为4,对角线AC、BD交于点O,点E是BC边上任意一点,分别向BD、AC作垂线,垂足分别为F、G,则四边形OFEG的周长是_____.
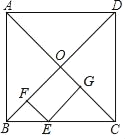
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com