
 如图,小明在楼上点A处观察旗杆BC,测得旗杆顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面的高AD为12m,求旗杆的高度.($\sqrt{2}$=1.414,$\sqrt{3}$=1.732,结果保留整数)
如图,小明在楼上点A处观察旗杆BC,测得旗杆顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面的高AD为12m,求旗杆的高度.($\sqrt{2}$=1.414,$\sqrt{3}$=1.732,结果保留整数) 分析 过A作AE⊥BC于E,在Rt△ACE中,已知了CE的长,可利用俯角∠CAE的正切函数求出AE的值;进而在Rt△ABE中,利用仰角∠BAE的正切函数求出BE的长;BC=BE+CE.
解答 解:过A作AE⊥BC于E.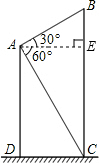
∵AD∥CE,
∴Rt△ACE中,CE=AD=12m,∠CAE=60°,
∴AE=CE÷tan60°=4$\sqrt{3}$.
Rt△AEB中,AE=4$\sqrt{3}$,∠BAE=30°,
∴BE=AE•tan30°=4.
BC=BE+CE=4+12=16米.
答:旗杆高16米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,首先构造直角三角形,再运用三角函数的定义解题,是中考常见题型,解题的关键是作出高线构造直角三角形.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
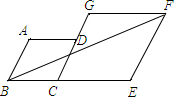 如图,在菱形ABCD和菱形CEFG中,B、C、E三点在一条直线上,C、D、G三点在一条直线上,若菱形ABCD边长为3,则当菱形CEFG的边长为$\frac{3+3\sqrt{5}}{2}$时,AG∥BF.
如图,在菱形ABCD和菱形CEFG中,B、C、E三点在一条直线上,C、D、G三点在一条直线上,若菱形ABCD边长为3,则当菱形CEFG的边长为$\frac{3+3\sqrt{5}}{2}$时,AG∥BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象经过点(1,1) | B. | 当x>0时,y随着x的增大而减小 | ||
| C. | 当x>0时,0<y<1 | D. | 图象位于第一、三象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com