考点:解一元一次不等式组,解分式方程,在数轴上表示不等式的解集,解一元一次不等式
专题:
分析:(1)首先去分母,然后去括号、移项、合并同类项、系数化成1即可求解;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集;
(3)去分母,去括号、然后移项、合并同类项、系数化成1,即可求得x的值,然后进行检验即可.
解答:解:(1)去分母,得:7(4-x)-21≤3(1-2x),
去括号,得:28-7x-21≤3-6x,
移项,得:6x-7x≤3-28+21,
合并同类项,得:-x≤-4,
系数化成1得:x≥4.

;
(2)
,
解①得:x≥-1,
解②得:x<3,
则不等式组的解集是:-1≤x<3.
则整数解是:-1,0,1,2;
(3)去分母,得:x-1+2(x+1)=4,
解得:x=1.
检验:当x=1时,x2-1=0,则x=1是增根,方程无解.
点评:本题考查了不等式组的解法,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

 ;
;

 阅读快车系列答案
阅读快车系列答案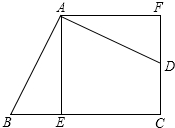 如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△BEA旋转后能与△DFA重合.
如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△BEA旋转后能与△DFA重合.