
【题目】已知![]() 中,D、E分别在AB、AC上,下列条件中,能推断
中,D、E分别在AB、AC上,下列条件中,能推断![]() 与
与![]() 相似的有( )个
相似的有( )个
①∠BDE+∠C=180°;②![]() ;③
;③![]() ;④∠A=90°,且
;④∠A=90°,且![]()
A.1B.2C.3D.4
【答案】C
【解析】
根据图形得到∠A是公共角,然后根据相似三角形的判定方法进行判断即可.
由图可知,
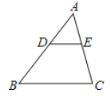
∠A是△ADE与△ACB的公共角,
①∵∠BDE+∠C=180°,∠ADE+∠BDE=180°,
∴∠ADE=∠C,
利用“两组角对应相等,两三角形相似”得到△ADE与△ACB相似;
②由ADAB=AEAC得到![]() ,可以利用“两边对应成比例,夹角相等,两三角形相似”得到△ADE与△ACB相似;
,可以利用“两边对应成比例,夹角相等,两三角形相似”得到△ADE与△ACB相似;
③由ADBC=ABDE可得到![]() ,公共角不是夹角,不能得到△ADE与△ACB相似;
,公共角不是夹角,不能得到△ADE与△ACB相似;
④∵![]() ,∠A=90°,
,∠A=90°,
利用“斜边和一条直角边对应成比例的两个直角三角形相似”得到△ADE与△ACB相似,
综上所述,能判断△ADE与△ACB相似的是①②④,共3个.
故选:C.


科目:初中数学 来源: 题型:
【题目】两个工程队共同参与一项筑路工程,若先由甲、乙两队合作![]() 天,剩下的工程再由乙队单独做
天,剩下的工程再由乙队单独做![]() 天可以完成,共需施工费
天可以完成,共需施工费![]() 万元;若由甲、乙合作完成此项工程共需
万元;若由甲、乙合作完成此项工程共需![]() 天,共需施工费
天,共需施工费![]() 万元.
万元.
(1)求乙队单独完成这项工程需多少天?
(2)甲、乙两队每天的施工费各为多少万元?
(3)若工程预算的总费用不超过![]() 万元,则乙队最少施工多少天?
万元,则乙队最少施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与x轴交于点A
的图像与x轴交于点A![]() ,B
,B![]() ,与y轴交于点C,其对称轴与x轴交于点D.
,与y轴交于点C,其对称轴与x轴交于点D.
(1)求二次函数的解析式及其对称轴;
(2)若点E是线段BC上的一点,过点E作x轴的垂线,垂足为F,且EF=2EC,求点E的坐标;
(3)若点P是抛物线对称轴上的一个动点,连接PA,PC,设点P的纵坐标为t,当∠APC不小于60°时,求t的取值范围.
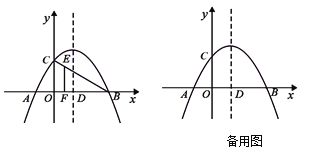
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在等腰![]() 中,如图①,在等腰
中,如图①,在等腰![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .点
.点![]() 为线段
为线段![]() 上一点(不与端点
上一点(不与端点![]() 、
、![]() 重合),
重合),![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
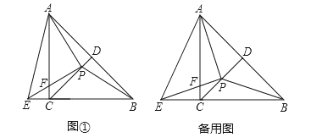
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)探究线段![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B=60°,AB=2,M为边AB的中点,N为边BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE、CE,当△CDE为等腰三角形时,BN的长为_____.
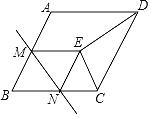
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.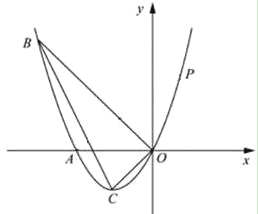
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】"桃花流水窅然去,别有天地非人间."桃花园景点2017年三月共接待游客![]() 万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加
万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加![]() ,则可列方程为( )
,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位数![]() ,如果千位与十位上的数字之和为7,百位与个位上的数字之和也为7,那么称
,如果千位与十位上的数字之和为7,百位与个位上的数字之和也为7,那么称![]() 为“上进数”.
为“上进数”.
(1)写出最小和最大的“上进数”;
(2)一个“上进数”![]() ,若
,若![]() ,且使一元二次方程
,且使一元二次方程![]() 有两个不相等的实数根,求这个“上进数”.
有两个不相等的实数根,求这个“上进数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com