
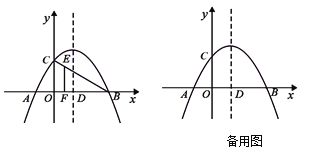
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与x轴交于点A
的图像与x轴交于点A![]() ,B
,B![]() ,与y轴交于点C,其对称轴与x轴交于点D.
,与y轴交于点C,其对称轴与x轴交于点D.
(1)求二次函数的解析式及其对称轴;
(2)若点E是线段BC上的一点,过点E作x轴的垂线,垂足为F,且EF=2EC,求点E的坐标;
(3)若点P是抛物线对称轴上的一个动点,连接PA,PC,设点P的纵坐标为t,当∠APC不小于60°时,求t的取值范围.
【答案】(1)![]() ,对称轴为:直线
,对称轴为:直线![]() ;(2)
;(2)![]() ;(3)0≤t≤2.
;(3)0≤t≤2.
【解析】
(1)将A,B两点坐标代入到二次函数解析式中进行求解;
(2)有多种方法进行求解,如根据△BFF∽△BCO,求出EF的长度,即求出E点纵坐标,将E点纵坐标代入到BC直线解析式后,求出其横坐标即可得到E点坐标.
(3)引入圆,分点圆上,内,外进行分析.
(1)将A(![]() ,0),B(
,0),B(![]() ,0)代入
,0)代入![]() 得
得
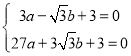
解得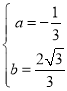 ,∴
,∴![]()
对称轴为:直线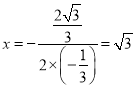 .
.
(2)如图所示.
∵CO⊥x轴,EF⊥x轴,
∴CO//EF.
∴△BEF∽△BCO.
∴![]() .
.
设EC=m,则EF=2m.
由B(![]() ,0),C(0,3)得BC=
,0),C(0,3)得BC=![]() .
.
∴![]() .
.
解得![]() .
.
∴![]() .
.
又由![]() 得
得![]() ,∴OF=
,∴OF=![]() =
=![]() .
.
∴![]()
解法二:由B(![]() ,0),C(0,3)得BC=
,0),C(0,3)得BC=![]() ,∴∠OBC=30,
,∴∠OBC=30,
设EC=m,则EF=2m,EB=6-m.
∴![]() ,解得
,解得![]()
![]() .
.
∴![]()
![]() .
.
利用三角函数求得BF=EF÷tan 30°=![]() ,∴OF=
,∴OF=![]()
![]() =
=![]()
∴![]()
解法三:求出![]() 后,即E点的纵坐标为
后,即E点的纵坐标为![]() ,
,
由B(![]() ,0),C(0,3)得直线BC解析式为
,0),C(0,3)得直线BC解析式为![]() ,
,
将yE=![]() 代入
代入![]() 得xE=
得xE=![]() ,∴
,∴![]() (解法二、解法三参考解法一相应步骤给分)
(解法二、解法三参考解法一相应步骤给分)
(3)如图2,由题意知∠CAO=60
作∠CAO的平分线AQ,交y轴于Q
则∠QAC=∠QCA=30
∴∠AQC=120
以Q为圆心,QA为半径作圆,与抛物线对称轴交于点M1,M2
当点M在圆上时,则∠AM1C=∠AM2C=![]() ∠AQC=60.
∠AQC=60.
当点M在圆内时,∠AMC>60,
当点M在圆外时,∠AMC<60,
过Q作QH垂直于对称轴.在Rt△AOQ中,求得AQ=2,
在Rt△M1QH中,M1H=![]()
∴M1D=1+1=2,M2D=1-1=0
∴0≤t≤2.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+4与x轴交于点B,与y轴交于点C,抛物线y=﹣x2+bx+c经过B,C两点,与x轴另一交点为A.点P以每秒![]() 个单位长度的速度在线段BC上由点B向点C运动(点P不与点B和点C重合),设运动时间为t秒,过点P作x轴垂线交x轴于点E,交抛物线于点M.
个单位长度的速度在线段BC上由点B向点C运动(点P不与点B和点C重合),设运动时间为t秒,过点P作x轴垂线交x轴于点E,交抛物线于点M.
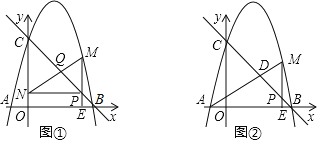
(1)求抛物线的解析式;
(2)如图①,过点P作y轴垂线交y轴于点N,连接MN交BC于点Q,当![]() 时,求t的值;
时,求t的值;
(3)如图②,连接AM交BC于点D,当△PDM是等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因“抗击疫情”需要,学校决定再次购进一批医用一次性口罩及KN95口罩共1000只,已知1只医用一次性口罩和10只KN95口罩共需113元;3只医用一次性口罩和5只KN95口罩共需64元.问:
(1)一只医用一次性口罩和一只KN95口罩的售价分别是多少元?
(2)参照上次购买获得的需求情况后,校长给出了一条建议:医用一次性口罩的购买量不能多于KN95口罩数量的2倍,请你遵循校长建议给出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABC进行位似变换得到△A1B1C1.
(1)△ABC与△A1B1C1的位似比是 .
(2)画出△ABC绕点O逆时针旋转180°得到的△A2B2C2.
(3)若点P(a,b)为△ABC内一点,求点P在△A2B2C2内的对应点P2的坐标.
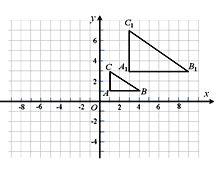
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
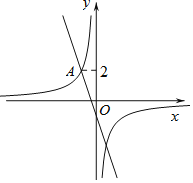
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
![]() 求双曲线
求双曲线![]() 的表达式;
的表达式;
![]() 过动点
过动点![]() 且垂直于x轴的直线与直线
且垂直于x轴的直线与直线![]() 及双曲线
及双曲线![]() 的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,D、E分别在AB、AC上,下列条件中,能推断
中,D、E分别在AB、AC上,下列条件中,能推断![]() 与
与![]() 相似的有( )个
相似的有( )个
①∠BDE+∠C=180°;②![]() ;③
;③![]() ;④∠A=90°,且
;④∠A=90°,且![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于 .
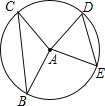
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com