
����Ŀ���������顱��Ҫ��ѧУ�����ٴι���һ��ҽ��һ���Կ��ּ�KN95���ֹ�1000ֻ����֪1ֻҽ��һ���Կ��ֺ�10ֻKN95���ֹ���113Ԫ��3ֻҽ��һ���Կ��ֺ�5ֻKN95���ֹ���64Ԫ���ʣ�
��1��һֻҽ��һ���Կ��ֺ�һֻKN95���ֵ��ۼ۷ֱ��Ƕ���Ԫ��
��2�������ϴι����õ����������У��������һ�����飺ҽ��һ���Կ��ֵĹ��������ܶ���KN95����������2����������ѭУ�����������ʡǮ�Ĺ�������˵�����ɣ�
���𰸡���1��һֻҽ��һ���Կ��ֵ��ۼ�Ϊ3Ԫ��һֻKN95���ֵ��ۼ�Ϊ11Ԫ����2����ʡǮ�Ĺ����ǣ�����666ֻҽ��һ���Կ��֣�334ֻKN95���֣����ɼ�������
��������
��1����һֻҽ��һ���Կ��ֵ��ۼ�ΪxԪ��һֻKN95���ֵ��ۼ�ΪyԪ��Ȼ����������г�������⼴�ɣ�
��2���蹺��mֻҽ��һ���Կ��֣�����1000��m��ֻKN95���֣������������m��ȡֵ��Χ���ٸ����ܼ�=���ۡ������ó������ܼ۵Ľ���ʽ�����ɸ��ݽ���ʽ�����ֵ���Ӷ��ó����������
��1����һֻҽ��һ���Կ��ֵ��ۼ�ΪxԪ��һֻKN95���ֵ��ۼ�ΪyԪ��
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
��һֻҽ��һ���Կ��ֵ��ۼ�Ϊ3Ԫ��һֻKN95���ֵ��ۼ�Ϊ11Ԫ��
��2���蹺��mֻҽ��һ���Կ��֣�����1000��m��ֻKN95���֣�
�����⣬�ã�m��2��1000��m����
��ã�m��666![]() ��
��
��ѧУ�ٴι���1000ֻ���ֵ��ܷ���ΪwԪ��
��w��3m+11��1000��m������8m+11000��
�ߩ�8��0��
��w��m�����������
�֡�m��������
��m�����ֵΪ666��
�൱m��666ʱ��wȡ����Сֵ����СֵΪ5672����ʱ1000��m��334��
����ʡǮ�Ĺ����ǣ�����666ֻҽ��һ���Կ��֣�334ֻKN95���֣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ѧ��У���ʦ��������ȫ��ͬ��ֽƬ��ֽƬ�Ϸֱ�д����ͼ��ʾͼ�ε�һ����������AD��BC����AB��DC����AO=OC��С��ͬѧ������ֽƬ�������ȡ���ţ���������״ͼ������ʾ����ȡ����ֽƬ�ϵ��������п��ܳ��ֵĽ��������ű�ʾ��������������������ı���ABCD��ƽ���ı��εĸ��ʣ�
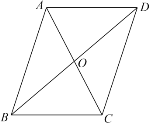
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() ���ң�
���ң�
��1����ͼ�٣�����![]() ����
����![]() ����
����![]() �Ĵ�С��
�Ĵ�С��
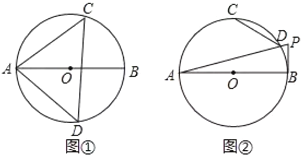
��2����ͼ�ڣ�![]() �ǰ�Բ��
�ǰ�Բ��![]() ���е㣬
���е㣬![]() ���ӳ��������
���ӳ��������![]() �������ཻ�ڵ�
�������ཻ�ڵ�![]() ����
����![]() ����
����![]() �Ĵ�С��
�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������̶ӹ�ͬ����һ����·���̣������ɼס������Ӻ���![]() �죬ʣ�µĹ��������Ҷӵ�����
�죬ʣ�µĹ��������Ҷӵ�����![]() �������ɣ�����ʩ����
�������ɣ�����ʩ����![]() ��Ԫ�����ɼס��Һ�����ɴ���̹���
��Ԫ�����ɼס��Һ�����ɴ���̹���![]() �죬����ʩ����
�죬����ʩ����![]() ��Ԫ��
��Ԫ��
��1�����Ҷӵ�����������������죿
��2���ס�������ÿ���ʩ���Ѹ�Ϊ������Ԫ��
��3��������Ԥ����ܷ��ò�����![]() ��Ԫ�����Ҷ�����ʩ�������죿
��Ԫ�����Ҷ�����ʩ�������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�E��BC�ӳ�����һ�㣬��AB��ȡһ��F��ʹ��B����ֱ��EF�ĶԳƵ�G����AD�ϣ�����EG��CD�ڵ�H������BH��EF�ڵ�M������CM�������н��ۣ�������ȷ���ǣ�������
����1����2��
����3����4��
��GD��![]() CM��
CM��
����AG��1��GD��2����BM��![]() ��
��
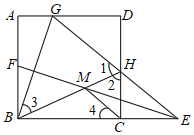
A.�٢ڢۢ�B.�٢�C.�ۢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ�����������·�����һ�������е�ˮ����ƽ���ۼ�Ϊ10Ԫ/ǧ�ˣ���������Ϊ1000ǧ��.���г����飬��������ˮ���۸������xԪ/ǧ�ˣ����·�������y��ǧ�ˣ���x��Ԫ/ǧ�ˣ�֮�����һ�κ�����ϵ�����ҵõ��˱��е����ݣ�
�۸�x��Ԫ/ǧ�ˣ� | 7 | 5 |
�۸�y��ǧ�ˣ� | 2000 | 4000 |
��1����y��x֮��ĺ�������ʽ��
��2����֪����ˮ�����·ݵijɱ���Ϊ5Ԫ/ǧ�ˣ����·ݵijɱ���Ϊ4Ԫ/ǧ�ˣ�Ҫʹ���·����۸���ˮ��������������·�����20����ͬʱ��Ҫ�ù˿͵õ�ʵ�ݣ���ô����ˮ���۸�ÿǧ��Ӧ����������Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ŷ���ƻ�����A��B������Ṳ42����Ϊ��ҵ��Ʒ����֪A�����ĵ��۱�B�ֵĶ�10Ԫ����4��A���������5��B�����ķ�����ͬ��
��1����A��B�������ĵ��۷ֱ��Ƕ���Ԫ��
��2������ѧ�����������ϲ�ò�ͬ���������֪�������A����������Ҫ����B�����������![]() �����ֲ�����B�����������
�����ֲ�����B�����������![]() ���������A�����x�ᣮ
���������A�����x�ᣮ
���ж����ֲ�ͬ�Ĺ�����
���̵�Ϊ�˴�����������A�����ÿ������aԪ���ۣ�12��a��18����B�����ÿ������bԪ���ۣ�����ί��ͬѧ�ڸ���ʱ���֣�����������ܷ����빺��ķ����أ����ܷ�������ʱ�����ʱa��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����x�ύ�ڵ�A
��ͼ����x�ύ�ڵ�A![]() ��B
��B![]() ����y�ύ�ڵ�C����Գ�����x�ύ�ڵ�D��
����y�ύ�ڵ�C����Գ�����x�ύ�ڵ�D��
��1������κ����Ľ���ʽ����Գ��
��2������E���߶�BC�ϵ�һ�㣬����E��x��Ĵ��ߣ�����ΪF����EF=2EC�����E�����ꣻ
��3������P�������߶Գ����ϵ�һ�����㣬����PA��PC�����P��������Ϊt������APC��С��60��ʱ����t��ȡֵ��Χ��
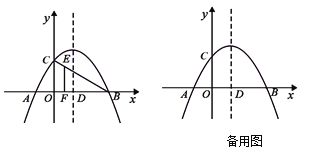
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����߾���A����2��0����B����3��3����ԭ��O������ΪC��
��1���������ߵĽ���ʽ��
��2������D���������ϣ���E�������ߵĶԳ����ϣ���A��O��D��EΪ������ı�����ƽ���ı��Σ����D�����ꣻ
��3��P���������ϵĵ�һ�����ڵĶ��㣬����P��PMx�ᣬ����ΪM���Ƿ���ڵ�P��ʹ����P��M��AΪ�������������BOC���ƣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�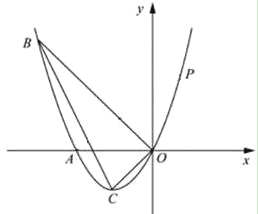
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com