
����Ŀ���Ŷ���ƻ�����A��B������Ṳ42����Ϊ��ҵ��Ʒ����֪A�����ĵ��۱�B�ֵĶ�10Ԫ����4��A���������5��B�����ķ�����ͬ��
��1����A��B�������ĵ��۷ֱ��Ƕ���Ԫ��
��2������ѧ�����������ϲ�ò�ͬ���������֪�������A����������Ҫ����B�����������![]() �����ֲ�����B�����������
�����ֲ�����B�����������![]() ���������A�����x�ᣮ
���������A�����x�ᣮ
���ж����ֲ�ͬ�Ĺ�����
���̵�Ϊ�˴�����������A�����ÿ������aԪ���ۣ�12��a��18����B�����ÿ������bԪ���ۣ�����ί��ͬѧ�ڸ���ʱ���֣�����������ܷ����빺��ķ����أ����ܷ�������ʱ�����ʱa��ֵ��
���𰸡���1��A�����ĵ���Ϊ50Ԫ��B�����ĵ���Ϊ40Ԫ����2����x��ȡ12��13��14��15��16��17����6�ֲ�ͬ�Ĺ�������18��
��������
(1)��A�����ĵ���ΪmԪ��B�����ĵ���ΪnԪ�����ݡ�A�����ĵ��۱�B�ֵĶ�10Ԫ����4��A���������5��B�����ķ�����ͬ�������ɵó�����m��n�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
(2)�����ݡ������A����������Ҫ����B�����������![]() �����ֲ�����B�����������
�����ֲ�����B�����������![]() �������ɵó�����x��һԪһ�β���ʽ�飬��֮���ɵó�x��ȡֵ��Χ���ٽ��xΪ���������ɵó�x�Ŀ���ֵ�������ɵó�������������
�������ɵó�����x��һԪһ�β���ʽ�飬��֮���ɵó�x��ȡֵ��Χ���ٽ��xΪ���������ɵó�x�Ŀ���ֵ�������ɵó�������������
���蹺���ܷ���ΪwԪ�������ܼۣ����ۡ����������ɵó�w����x�ĺ�����ϵʽ���ɹ���������ܷ����빺��ķ����ؿɵó�b��a��10�������ɵó�w����a�ĺ�����ϵʽ��������һ�κ��������ʣ����ɽ����ֵ���⣮
�⣺��1����A�����ĵ���ΪmԪ��B�����ĵ���ΪnԪ��
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
��A�����ĵ���Ϊ50Ԫ��B�����ĵ���Ϊ40Ԫ��
��2�������ݹ����A����������Ҫ����B�����������![]() �����ֲ�����B�����������
�����ֲ�����B�����������![]() �ã�
�ã�
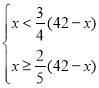 ��
��
��ã�12��x��18��
�֡�xΪ��������
��x��ȡ12��13��14��15��16��17����6�ֲ�ͬ�Ĺ�����
���蹺���ܷ���ΪwԪ��
������ã�w��(50��a��x+(40��b)(42��x)��(10��a+b)x+42(40��b)��
�߹���������ܷ����빺��ķ����أ���w��ֵ��x�أ�
��10��a+b��0��
��b��a��10��
��w��42(40-b)��42[40-(a-10)]����42a+2100��
�ߩ�42��0��
��w��a�����������
�֡�12��a��18��
�൱a��18ʱ��wȡ����Сֵ��
�𣺵��ܷ�������ʱ��a��ֵΪ18��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������龳���ڡ�ABC�У�BA��BC����ABC������0�㣼����180�㣩����PΪֱ��BC��һ���㣨�����B��C�غϣ�������AP�����߶�PA�Ƶ�P˳ʱ����ת�õ��߶�PQ��ת��Ϊ��������CQ��
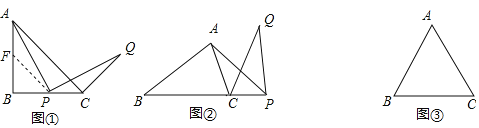
��������������1��������90�㣬��P���߶�BC��ʱ����P��PF��AC��ֱ��AB�ڵ�F����ͼ������ͼ�����APFȫ�ȵ�һ������������ ����ACQ���� ���㣮
����չ̽������2������P��BC�ӳ����ϣ�AB��AC��m��nʱ����ͼ���������߶�BP��CQ�ı�ֵ��
������������3������P��ֱ��BC�ϣ�����60�㣬��APB��30�㣬CP��4ʱ����ֱ��д���߶�CQ�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣬��������⣺
��ͼ��ʾ��8��8�������ɱ߳�Ϊ1��С��������ɣ�ͼ���е�ͼ����3�����ҹ���������ˬ��ע�⡶�����㾭��ʱ�����ģ����dz���Ϊ����ˬ��ͼ������ˬͨ��������ͼ���иƴ�ӣ���������������ϵ֤���������Ĺ��ɶ��������������ҹ����˶���ѧ�����о���ʹ������ǣ����ҹ���ѧʷ�ϵĽ�����

���⣺
���á���ˬ��ͼ���е��ĸ�ֱ��������ͨ������ѧ����ͼ�α仯����ͼ�ڣ�ͼ�۵ķ���ֽ���������������ͬ��ͼ����ÿ��ֱ�������εĶ�����ڷ���ֽ�ĸ���ϣ����ĸ������λ����ص�����ͼҪ��
��1��ͼ��������Ƶ�ͼ������������ֽ����������Գ�ͼ�ε��������ĶԳ�ͼ�Σ�
��2��ͼ��������Ƶ�ͼ������������ֽ�����������Գ�ͼ�Σ��������ĶԳ�ͼ�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������顱��Ҫ��ѧУ�����ٴι���һ��ҽ��һ���Կ��ּ�KN95���ֹ�1000ֻ����֪1ֻҽ��һ���Կ��ֺ�10ֻKN95���ֹ���113Ԫ��3ֻҽ��һ���Կ��ֺ�5ֻKN95���ֹ���64Ԫ���ʣ�
��1��һֻҽ��һ���Կ��ֺ�һֻKN95���ֵ��ۼ۷ֱ��Ƕ���Ԫ��
��2�������ϴι����õ����������У��������һ�����飺ҽ��һ���Կ��ֵĹ��������ܶ���KN95����������2����������ѭУ�����������ʡǮ�Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ּҵ�ϴ��̨������һƿϴ��Һ����ͼ1�������ְ�ס����A��ѹʱ����ͼ2����ϴ��Һ˲������B��������֪ƿ���ϲ��ֵ�![]() ��
��![]() ��Բ�ķֱ�ΪD��C���²��ֵ���ͼ�Ǿ���CGHD��GH��10cm��GC��8cm����E��̨��GH�ľ���Ϊ14cm����B��̨��GH�ľ���Ϊ16cm����B��D��H���㹲�ߣ���������B������ϴ��Һ·�߳��������Σ��Ҹ�·�����ڵ������߾���C��E���㣬��ϴ��Һʱ��������O��DH��ˮƽ����Ϊ2cmʱ������O��ˮƽ̨��GH�ĸ߶�Ϊ_____cm��
��Բ�ķֱ�ΪD��C���²��ֵ���ͼ�Ǿ���CGHD��GH��10cm��GC��8cm����E��̨��GH�ľ���Ϊ14cm����B��̨��GH�ľ���Ϊ16cm����B��D��H���㹲�ߣ���������B������ϴ��Һ·�߳��������Σ��Ҹ�·�����ڵ������߾���C��E���㣬��ϴ��Һʱ��������O��DH��ˮƽ����Ϊ2cmʱ������O��ˮƽ̨��GH�ĸ߶�Ϊ_____cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ��![]() ���������ν�ֱ��a��b�ڵ�A��B��C�͵�D��E��F.
���������ν�ֱ��a��b�ڵ�A��B��C�͵�D��E��F.
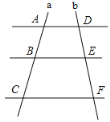
��1�����![]() ��
��![]() ��
��![]() ����DE�ij�.
����DE�ij�.
��2�����![]() ��
��![]() ��
��![]() ����BE�ij�.
����BE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
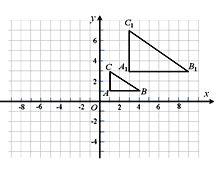
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABC����λ�Ʊ任�õ���A1B1C1��
��1����ABC���A1B1C1��λ�Ʊ�������������
��2��������ABC�Ƶ�O��ʱ����ת180��õ��ġ�A2B2C2��
��3������P(a��b)Ϊ��ABC��һ�㣬���P�ڡ�A2B2C2�ڵĶ�Ӧ��P2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
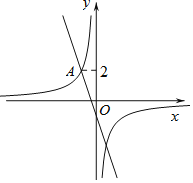
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��![]() ��˫����
��˫����![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��
![]() ��˫����
��˫����![]() �ı���ʽ��
�ı���ʽ��
![]() ������
������![]() �Ҵ�ֱ��x���ֱ����ֱ��
�Ҵ�ֱ��x���ֱ����ֱ��![]() ��˫����
��˫����![]() �Ľ���ֱ�ΪB��C������Bλ�ڵ�C�·�ʱ�����n��ȡֵ��Χ��
�Ľ���ֱ�ΪB��C������Bλ�ڵ�C�·�ʱ�����n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���Ӫһ����Ʒ��������ÿǧ��30Ԫ�������г����鷢�֣�ÿ�յ�������![]() ��ǧ�ˣ����ۼ�
��ǧ�ˣ����ۼ�![]() ��Ԫ/ǧ�ˣ�����һ�κ�����ϵ���±���¼����ij���յ��й����ݣ�
��Ԫ/ǧ�ˣ�����һ�κ�����ϵ���±���¼����ij���յ��й����ݣ�
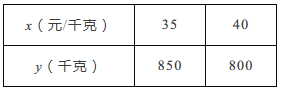
��1����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�������۹��������۵��۲����ڳɱ��ۣ��Ҳ�����80Ԫ��ij�ո��̳�����������Ʒ�����14000Ԫ�����������Ʒ���ۼۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com