
【题目】(问题情境)在△ABC中,BA=BC,∠ABC=α(0°<α<180°),点P为直线BC上一动点(不与点B、C重合),连接AP,将线段PA绕点P顺时针旋转得到线段PQ旋转角为α,连接CQ.
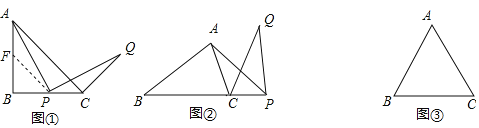
(特例分析)(1)当α=90°,点P在线段BC上时,过P作PF∥AC交直线AB于点F,如图①,易得图中与△APF全等的一个三角形是 ,∠ACQ= °.
(拓展探究)(2)当点P在BC延长线上,AB:AC=m:n时,如图②,试求线段BP与CQ的比值;
(问题解决)(3)当点P在直线BC上,α=60°,∠APB=30°,CP=4时,请直接写出线段CQ的长.
【答案】(1)△PQC,90;(2)![]() ;(3)线段CQ的长为2或8.
;(3)线段CQ的长为2或8.
【解析】
(1)△ABC是等腰直角三角形,PF∥AC,得到△BPF是等腰直角三角形,证明AF=CP,利用旋转的旋转证明AP=PQ,∠PAF=∠QPC,从而可得结论,
(2)过P作PF∥AC,交BA的延长线于F,则![]() ,再证明△AFP≌△PCQ,利用△ABC∽△FBP的性质可得答案,
,再证明△AFP≌△PCQ,利用△ABC∽△FBP的性质可得答案,
(3)分情况讨论:当P在CB的延长线上时,证明△APC≌△QPC,利用等边三角形的性质可得答案,当P在BC的延长线上时,连接AQ,利用等边三角形的性质,证明△ACQ≌△PCQ,从而可得答案.
解:(1)如图①,∵∠ABC=90°,AB=CB,
∴△ABC是等腰直角三角形,
∵PF∥AC,
∴∠BPF=∠BFP=45°,
∴△BPF是等腰直角三角形,
∴BF=BP,
∴AF=CP,
由旋转可得,AP=PQ,∠APQ=90°,而∠BPF=45°,
∴∠QPC=45°﹣∠APF,
又∵∠PAF=∠PFB﹣∠APF=45°﹣∠APF,
∴∠PAF=∠QPC,
∴△APF≌△PQC,
∴∠PCQ=∠AFP=135°,
又∵∠ACB=45°,
∴∠ACQ=90°,
故答案为:△PQC,90;
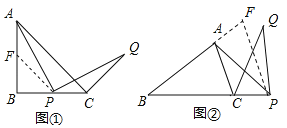
(2)如图②,过P作PF∥AC,交BA的延长线于F,则![]() ,
,
又∵AB=BC,
∴AF=CP,
又∵∠FAP=∠ABC+∠APB=α+∠APB,∠CPQ=∠APQ+∠APB=α+∠APB,
∴∠FAP=∠CPQ,
由旋转可得,PA=PQ,
∴△AFP≌△PCQ,
∴FP=CQ,
∵PF∥AC,
∴△ABC∽△FBP,
∴![]() ,
,
![]()
∴![]()
(3)如图,当P在CB的延长线上时,
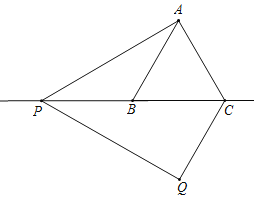
∠CPQ=∠APQ﹣∠APB=60°﹣30°=30°,
∴∠APC=∠QPC,
又∵AP=QP,PC=PC,
∴△APC≌△QPC,
∴CQ=AC,
又∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,∠BAP=∠ABC﹣∠APB=30°,
∴BP=AB=BC=![]() PC=2,
PC=2,
∴QC=AC=BC=2;
如图,当P在BC的延长线上时,连接AQ,
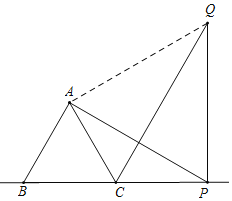
由旋转可得,AP=QP,∠APQ=∠ABC=60°,
∴△APQ是等边三角形,
∴AQ=PQ,∠APQ=60°=∠AQP,
又∵∠APB=30°,∠ACB=60°,
∴∠CAP=30°,∠CPQ=90°,
∴∠CAP=∠APA,
∴AC=PC,
∴△ACQ≌△PCQ,
∴∠AQC=∠PQC=![]() ∠AQP=30°,
∠AQP=30°,
∴Rt△PCQ中,CQ=2CP=8.
综上所述,线段CQ的长为2或8.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+px+q的对称轴为直线x=﹣2,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(﹣1,﹣1).若要在y轴上找一点P,使得PM+PN最小,则点P的坐标为( ).
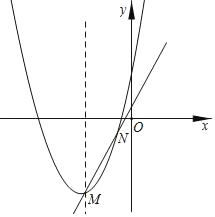
A. (0,﹣2) B. (0,﹣![]() ) C. (0,﹣
) C. (0,﹣![]() ) D. (0,﹣
) D. (0,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数图象的顶点坐标为C(1,﹣2),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,0),B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.
(1)求这个二次函数的解析式;
(2)设点P的横坐标为x,求线段PE的长(用含x 的代数式表示);
(3)点D为直线AB与这个二次函数图象对称轴的交点,若以点P、E、D为顶点的三角形与△AOB相似,请求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
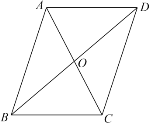
【题目】在一次数学活动中,老师准备三张完全相同的纸片,纸片上分别写有如图所示图形的一个条件:①AD=BC;②AB∥DC;③AO=OC,小明同学从三张纸片中任意抽取两张.请你用树状图或表格表示出抽取两张纸片上的条件所有可能出现的结果(用序号表示),并求出上述条件下四边形ABCD是平行四边形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生每周平均课外阅读时间(单位: ![]() ), 随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和②,请根据相关信息,解答下列问题;
), 随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和②,请根据相关信息,解答下列问题;
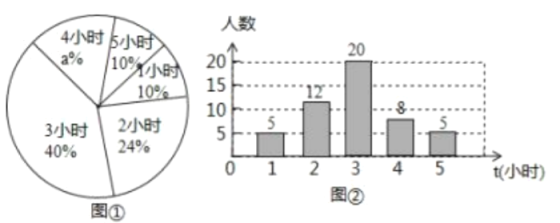
![]() 该校抽查九年级学生的人数为_______,图①中的 a值为______;
该校抽查九年级学生的人数为_______,图①中的 a值为______;
![]() 求统计的这组每周平均课外阅读时间的样本数据的平均数、众数和中位数;
求统计的这组每周平均课外阅读时间的样本数据的平均数、众数和中位数;
![]() 若该校九年级共有
若该校九年级共有![]() 名学生,根据统计的这组每周平均课外阅读时间的样本数据,估计该校九年级每周平均课外阅读时间为
名学生,根据统计的这组每周平均课外阅读时间的样本数据,估计该校九年级每周平均课外阅读时间为![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分已知关于x的一元二次方程(m-2)x2+(2m+1)x+m=0有两个实数根x1,x2.
(1)求m的取值范围.
(2)若|x1|=|x2|,求m的值及方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九二班计划购买A、B两种相册共42册作为毕业礼品,已知A种相册的单价比B种的多10元,买4册A种相册与买5册B种相册的费用相同.
(1)求A、B两种相册的单价分别是多少元?
(2)由于学生对两类相册喜好不同,经调查得知:购买的A种相册的数量要少于B种相册数量的![]() ,但又不少于B种相册数量的
,但又不少于B种相册数量的![]() ,如果设买A种相册x册.
,如果设买A种相册x册.
①有多少种不同的购买方案?
②商店为了促销,决定对A种相册每册让利a元销售(12≤a≤18),B种相册每册让利b元销售,最后班委会同学在付款时发现:购买所需的总费用与购买的方案无关,当总费用最少时,求此时a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com