
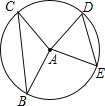
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于 .
科目:初中数学 来源: 题型:
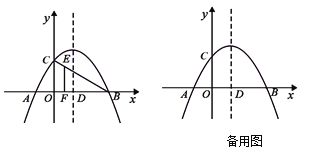
【题目】如图,在平面直角坐标系中,二次函数![]() 的图像与x轴交于点A
的图像与x轴交于点A![]() ,B
,B![]() ,与y轴交于点C,其对称轴与x轴交于点D.
,与y轴交于点C,其对称轴与x轴交于点D.
(1)求二次函数的解析式及其对称轴;
(2)若点E是线段BC上的一点,过点E作x轴的垂线,垂足为F,且EF=2EC,求点E的坐标;
(3)若点P是抛物线对称轴上的一个动点,连接PA,PC,设点P的纵坐标为t,当∠APC不小于60°时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.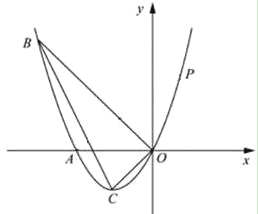
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】"桃花流水窅然去,别有天地非人间."桃花园景点2017年三月共接待游客![]() 万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加
万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加![]() ,则可列方程为( )
,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明星期天上午8:00从家出发到离家36千米的书城买书,他先从家出发骑公共自行车到公交车站,等了12分钟的车,然后乘公交车于9:48分到达书城(假设在整个过程中小明骑车的速度不变,公交车匀速行驶,小明家、公交车站、书城依次在一条笔直的公路旁).如图是小明从家出发离公交车站的路程y(千米)与他从家出发的时间x(时)之间的函数图象,其中线段AB对应的函教表达式为y=kx+6.
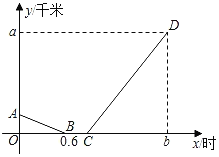
(1)求小明骑公共自行车的速度;
(2)求线段CD对应的函数表达式;
(3)求出发时间x在什么范围时,小明离公交车站的路程不超过3千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
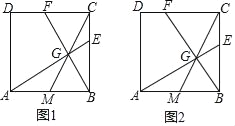
【题目】已知正方形ABCD,点M为边AB的中点.
(1)如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.
①求证:BE=CF;
②求证:BE2=BCCE.
(2)如图2,在边BC上取一点E,满足BE2=BCCE,连接AE交CM于点G,连接BG并延长交CD于点F,求tan∠CBF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
(1)求抛物线的解析式;
(2)观察图象,写出不等式ax2+bx+c>﹣x+3的解集为 ;
(3)若点D的坐标为(﹣1,0),在直线y=﹣x+3上有一点P,使△ABO与△ADP相似,求出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位数![]() ,如果千位与十位上的数字之和为7,百位与个位上的数字之和也为7,那么称
,如果千位与十位上的数字之和为7,百位与个位上的数字之和也为7,那么称![]() 为“上进数”.
为“上进数”.
(1)写出最小和最大的“上进数”;
(2)一个“上进数”![]() ,若
,若![]() ,且使一元二次方程
,且使一元二次方程![]() 有两个不相等的实数根,求这个“上进数”.
有两个不相等的实数根,求这个“上进数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() 为坐标原点.直线
为坐标原点.直线![]() 与抛物线
与抛物线![]() 同时经过
同时经过![]() .
.
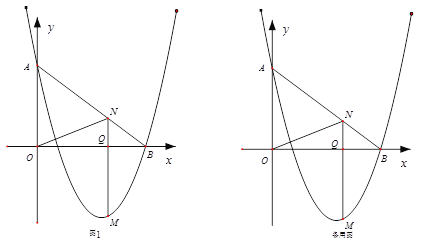
(1)求![]() 的值.
的值.
(2)点![]() 是二次函数图象上一点,(点
是二次函数图象上一点,(点![]() 在
在![]() 下方),过
下方),过![]() 作
作![]()
![]() 轴,与
轴,与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .求
.求![]() 的最大值.
的最大值.
(3)在(2)的条件下,是否存在点![]() ,使
,使![]() 和
和![]() 相似?若存在,求出
相似?若存在,求出![]() 点坐标,不存在,说明理由.
点坐标,不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com