
【题目】如图,已知直线y=﹣x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A、B、C(1,0)三点.
(1)求抛物线的解析式;
(2)观察图象,写出不等式ax2+bx+c>﹣x+3的解集为 ;
(3)若点D的坐标为(﹣1,0),在直线y=﹣x+3上有一点P,使△ABO与△ADP相似,求出点P的坐标.

【答案】(1)y=x2﹣4x+3;(2)x<0或x>3;(3)P1(﹣1,4),P2(1,2).
【解析】
(1)根据题意首先利用交点式得出y=a(x﹣1)(x﹣3),进而得出a的值即可;
(2)由题意直接利用函数图象得出ax2+bx+c>﹣x+3的解集即为交点两侧两图象在上面的则对应函数值大,否则就小,进而得出答案;
(3)根据题意分析①若△ABO∽△AP1D,②若△ABO∽△ADP2,进而分别得出P点坐标即可.
解:(1)由题意得出:A(3,0),B(0,3),
∵抛物线y=ax2+bx+c经过A、B、C(1,0)三点,
∴设y=a(x﹣1)(x﹣3),(a≠0),
∴a×(﹣1)×(﹣3)=3,
∴抛物线解析式为:y=x2﹣4x+3;
(2)∵A(3,0),B(0,3),
∴利用图象可得出:不等式ax2+bx+c>﹣x+3的解集为:x<0或x>3;
故答案为:x<0或x>3;
(3)由题意得:△ABO为等腰直角三角形,如图所示:
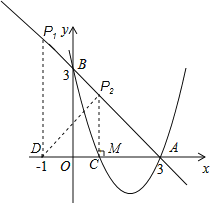
①若△ABO∽△AP1D,
则![]() =
=![]() ,
,
∴DP1=AD=4,
∴P1(﹣1,4);
②若△ABO∽△ADP2,过点P2作P2M⊥x轴于点M,AD=4,
∵△ABO为等腰直角三角形,
∴△ADP2是等腰直角三角形,由三线合一可得:DM=AM=2=P2M,
∴MO=1,
∴P2(1,2).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
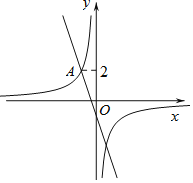
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
![]() 求双曲线
求双曲线![]() 的表达式;
的表达式;
![]() 过动点
过动点![]() 且垂直于x轴的直线与直线
且垂直于x轴的直线与直线![]() 及双曲线
及双曲线![]() 的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
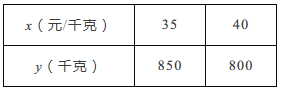
【题目】某商场经营一种商品,进价是每千克30元,根据市场调查发现,每日的销售量![]() (千克)与售价
(千克)与售价![]() (元/千克)满足一次函数关系,下表记录的是某两日的有关数据:
(元/千克)满足一次函数关系,下表记录的是某两日的有关数据:
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)在销售过程中销售单价不低于成本价,且不高于80元,某日该商场出售这种商品获得了14000元的利润,求该商品的售价?
查看答案和解析>>
科目:初中数学 来源: 题型:
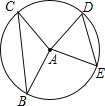
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),在![]() 中,分别作
中,分别作![]() 边上的高和中线,请用无刻度的直尺完成作图(保留作图痕迹);
边上的高和中线,请用无刻度的直尺完成作图(保留作图痕迹);
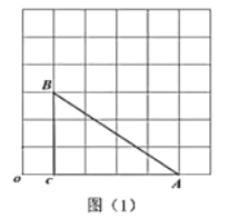
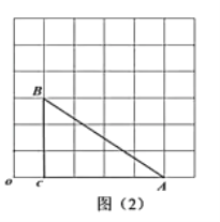
(2)如图(2),以![]() 为旋转中心,将
为旋转中心,将![]() 顺时针旋转
顺时针旋转![]() 度,得到
度,得到![]() 请用无刻度的直尺作出
请用无刻度的直尺作出![]() (保留作图痕迹).
(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小薇、小宇两同学用4张扑克牌(方块3、梅花4、梅花5、黑桃5)一起玩游戏,他两将扑克牌洗匀后,背面朝上放置在桌面上,小薇先随机在这四张扑克牌中抽取一张,然后小宇在剩余的扑克牌中随机抽取一张.
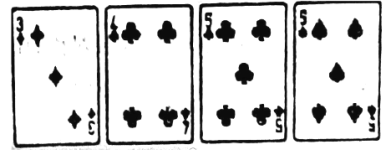
(1)求小薇抽出的牌面数字大于4的概率;
(2)小薇、小宇约定:若小薇抽到的牌面数字比小宇的大,则小薇赢;反之,则小薇输.请你用列表或画树状图的方法说明这个游戏对双方是否公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
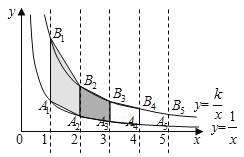
【题目】在滑草过程中,小明发现滑道两边形如两条双曲线,如图,点A1,A2,A3…在反比例函数y=![]() (x>0)的图象上,点B1,B2,B3…反比例函数y=
(x>0)的图象上,点B1,B2,B3…反比例函数y=![]() (k>1,x>0)的图象上,A1B1∥A2B2…∥y轴,已知点A1,A2…的横坐标分别为1,2,…,令四边形A1B1B2A2、A2B2B3A3、…的面积分别为S1、S2、….若S19=39,则k=__.
(k>1,x>0)的图象上,A1B1∥A2B2…∥y轴,已知点A1,A2…的横坐标分别为1,2,…,令四边形A1B1B2A2、A2B2B3A3、…的面积分别为S1、S2、….若S19=39,则k=__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com