
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§÷±œΏyΘΫx+4”κyΘΫkx+4Ζ÷±πΫΜx÷α”ΎΒψAΓΔBΘ§ΝΫ÷±œΏΫΜ”Ύy÷α…œΆ§“ΜΒψCΘ§ΒψDΒΡΉχ±ξΈΣ(©¹![]() Θ§0)Θ§ΒψE «ACΒΡ÷–ΒψΘ§Ν§Ϋ”OEΫΜCD”ΎΒψFΘ°
Θ§0)Θ§ΒψE «ACΒΡ÷–ΒψΘ§Ν§Ϋ”OEΫΜCD”ΎΒψFΘ°
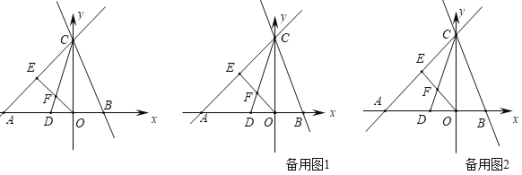
Θ®1Θ©«σΒψFΒΡΉχ±ξΘΜ
Θ®2Θ©»τΓœOCBΘΫΓœACDΘ§«σkΒΡ÷ΒΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§ΙΐΒψFΉςx÷αΒΡ¥ΙœΏ1Θ§ΒψM «÷±œΏBC…œΒΡΕ·ΒψΘ§ΒψN «x÷α…œΒΡΕ·ΒψΘ§ΒψP «÷±œΏl…œΒΡΕ·ΒψΘ§ ΙΒΟ“‘BΘ§PΘ§MΓΔNΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘ§«σΒψPΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©F(©¹1Θ§1)ΘΜΘ®2Θ©©¹2ΘΜΘ®3Θ©PΒΡΉχ±ξΈΣ(©¹1Θ§![]() )Μρ(©¹1Θ§
)Μρ(©¹1Θ§![]() )Μρ(©¹1Θ§©¹6)
)Μρ(©¹1Θ§©¹6)
ΓΨΫβΈωΓΩ
Θ®1Θ©«σ≥ω÷±œΏOEΘ§÷±œΏCDΒΡΫβΈω ΫΘ§ΙΙΫ®ΖΫ≥ΧΉιΦ¥Ω…ΫβΨωΈ ΧβΘ°
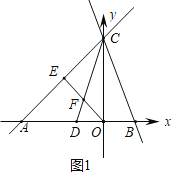
Θ®2Θ©»γΆΦ2÷–Θ§ΫΪœΏΕΈDC»ΤΒψDΥ≥ ±’κ–ΐΉΣ90ΓψΒΟΒΫDTΘ§Ής÷±œΏCTΫΜx÷α”ΎBΘ°÷ΛΟςΓœACOΘΫΓœDCBΘΫ45ΓψΘ§Φ¥Ω…ΆΤ≥ωΓœACDΘΫΓœOCBΘ§«σ≥ωΒψTΒΡΉχ±ξΘ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®Φ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®3Θ©»γΆΦ3÷–Θ§Ζ÷»ΐ÷÷«ι–ΈΘΚΒ±ΥΡ±Ώ–ΈBN1P1M1 «Νβ–Έ ±Θ§Β±ΥΡ±Ώ–ΈBN2P2M2 «Νβ–Έ ±Θ§Β±ΥΡ±Ώ–ΈBP3N3M3 «Νβ–Έ ±Θ§Ζ÷±π«σΫβΦ¥Ω…ΫβΨωΈ ΧβΘ°
ΫβΘΚΘ®1Θ©»γΆΦ1÷–Θ§
ΓΏ÷±œΏyΘΫx+4ΫΜx÷α”ΎAΘ§ΫΜy÷α”ΎCΘ§
ΓύAΘ®©¹4Θ§0Θ©Θ§CΘ®0Θ§4Θ©Θ§
ΓΏAEΘΫECΘ§
ΓΏEΘ®©¹2Θ§2Θ©Θ§
Γύ÷±œΏOEΒΡΫβΈω ΫΈΣyΘΫ©¹xΘ§
ΓΏ![]()
Γύ÷±œΏCDΒΡΫβΈω ΫΈΣyΘΫ3x+4Θ§
”…![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]()
ΓύFΘ®©¹1Θ§1Θ©Θ°
Θ®2Θ©»γΆΦ2÷–Θ§ΫΪœΏΕΈDC»ΤΒψDΥ≥ ±’κ–ΐΉΣ90ΓψΒΟΒΫDTΘ§Ής÷±œΏCTΫΜx÷α”ΎBΘ°
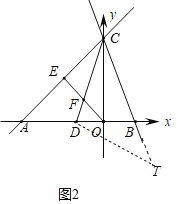
ΓΏDCΘΫDTΘ§ΓœCDTΘΫ90ΓψΘ§
ΓύΓœDCTΘΫ45ΓψΘ§
ΓΏOAΘΫOCΘ§ΓœAOCΘΫ90ΓψΘ§
ΓύΓœACOΘΫΓœDCTΘΫ45ΓψΘ§
ΓύΓœACDΘΫΓœOCBΘ§
ΓΏ![]()
Α―![]() ¥ζ»κyΘΫkx+4Θ§ΒΟΒΫkΘΫ©¹2Θ°
¥ζ»κyΘΫkx+4Θ§ΒΟΒΫkΘΫ©¹2Θ°
Θ®3Θ©»γΆΦ3÷–Θ§
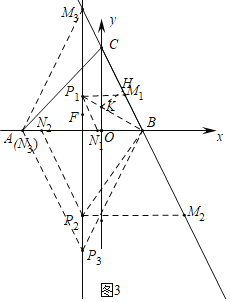
Β±ΥΡ±Ώ–ΈBN1P1M1 «Νβ–Έ ±Θ§Ν§Ϋ”BP1ΫΜOC”ΎKΘ§ΉςKHΓΆBC”ΎHΘ°
ΓΏΓœKBOΘΫΓœKBHΘ§KOΓΆOBΘ§KHΓΆBCΘ§
ΓύKOΘΫKHΘ§
ΓΏBKΘΫBKΘ§ΓœKOBΘΫΓœKHBΘΫ90ΓψΘ§
ΓύRtΓςKBOΓ’RtΓςKBHΘ®HLΘ©Θ§
ΓύBOΘΫBHΘΫ2Θ§…ηOKΘΫKHΘΫxΘ§
ΓΏ![]()
Γύ![]()
‘ΎRtΓςCHK÷–Θ§CK2ΘΫKH2+CH2Θ§
Γύ![]()
Γύ![]()
Γύ÷±œΏBKΒΡΫβΈω ΫΈΣ![]()
Β±xΘΫ©¹1 ±Θ§![]()
Γύ
Β±ΥΡ±Ώ–ΈBN2P2M2 «Νβ–Έ ±Θ§Ω…ΒΟ÷±œΏBP2ΒΡΫβΈω ΫΈΣ![]()
Β±xΘΫ©¹1 ±Θ§![]()
Γύ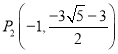
Β±ΥΡ±Ώ–ΈBP3N3M3 «Νβ–Έ ±Θ§M3‘Ύ÷±œΏxΘΫ©¹1 ±
ΓύM3Θ®©¹1Θ§6Θ©Θ§
ΓΏP3”κM3ΙΊ”Ύx÷αΕ‘≥ΤΘ§
ΓύP3Θ®©¹1Θ§©¹6Θ©Θ°
Ήέ…œΥυ ωΘ§¬ζΉψΧθΦΰΒΡΒψPΒΡΉχ±ξΈΣ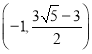 Μρ
Μρ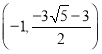 ΜρΘ®©¹1Θ§©¹6Θ©Θ°
ΜρΘ®©¹1Θ§©¹6Θ©Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΙΛ≥ßΡβΫ®“ΜΗω»γΆΦΥυ ΨΒΡΨΊ–Έ≤÷ΩβABCDΘ§≤÷ΩβΒΡ“Μ±Ώ «≥ΛΈΣ12mΒΡ“ΜΟφ«ΫΘ§ΝμΆβ»ΐ±Ώ”Ο30m≥ΛΒΡΫ®÷ΰ≤ΡΝœΈß≥…Θ°…ηABΒΡ≥ΛΈΣxmΘ§ΨΊ–ΈABCIΒΡΟφΜΐΈΣSm2Θ°
(1)”ΟΚ§xΒΡ¥ζ ΐ Ϋ±μ ΨBCΒΡ≥ΛΘ§≤Δ«σ≥ωxΒΡ»Γ÷ΒΖΕΈßΘ°
(2)–¥≥ωSΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωSΒΡΉν¥σ÷ΒΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐΒΡΆΦœσΨ≠ΙΐPΘ®2Θ§2Θ©Θ§ΕΞΒψΈΣOΘ®0Θ§0Θ©Θ§ΫΪΗΟΆΦœσœρ”“ΤΫ“ΤΘ§Β±Υϋ‘Ό¥ΈΨ≠ΙΐΒψP ±Θ§ΥυΒΟ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣΘ®ΓΓΓΓΘ©
A.yΘΫ![]() x2B.yΘΫ
x2B.yΘΫ![]() Θ®x©¹2Θ©2C.yΘΫ
Θ®x©¹2Θ©2C.yΘΫ![]() Θ®x©¹4Θ©2D.yΘΫ
Θ®x©¹4Θ©2D.yΘΫ![]() Θ®x©¹2Θ©2+2
Θ®x©¹2Θ©2+2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
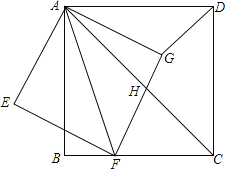
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈABCD÷–Θ§ΒψF «BC±Ώ…œ“ΜΒψΘ§Ν§ΫαAFΘ§“‘AFΈΣΕ‘Ϋ«œΏΉς’ΐΖΫ–ΈAEFGΘ§±ΏFG”κ’ΐΖΫ–ΈABCDΒΡΕ‘Ϋ«œΏACœύΫΜ”ΎΒψHΘ§Ν§ΫαDG.
(1)ΧνΩ’ΘΚ»τΓœBAFΘΫ18ΓψΘ§‘ρΓœDAGΘΫ______Γψ.
(2)÷ΛΟςΘΚΓςAFCΓΉΓςAGDΘΜ
(3)»τ![]() ΘΫ
ΘΫ![]() Θ§«κ«σ≥ω
Θ§«κ«σ≥ω![]() ΒΡ÷Β.
ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
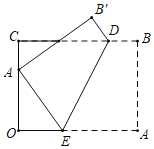
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–ΈOABC÷–Θ§OAΘΫ4Θ§ABΘΫ3Θ§ΒψD‘Ύ±ΏBC…œΘ§«“CDΘΫ3DBΘ§ΒψE «±ΏOA…œ“ΜΒψΘ§Ν§Ϋ”DEΘ§ΫΪΥΡ±Ώ–ΈABDE―ΊDE’έΒΰΘ§»τΒψAΒΡΕ‘≥ΤΒψAΓδ«ΓΚΟ¬δ‘Ύ±ΏOC…œΘ§‘ρOEΒΡ≥ΛΈΣΘ®ΓΓΓΓΘ©
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–ΘΈΣΝΥΫβΤΏΓΔΑΥΡξΦΕ―ß…ζ”Δ”οΧΐΝΠ―ΒΝΖ«ιΩωΘ®ΤΏΓΔΑΥΡξΦΕ―ß…ζ»Υ ΐœύΆ§Θ©Θ§Ρ≥÷ή¥”’βΝΫΗωΡξΦΕ―ß…ζ÷–Ζ÷±πΥφΜζ≥ι≤ιΝΥ30ΟϊΆ§―ßΘ§Βς≤ιΝΥΥϊΟ«÷ή“Μ÷Ν÷ήΈεΒΡΧΐΝΠ―ΒΝΖ«ιΩωΘ§ΗυΨίΒς≤ι«ιΩωΒΟΒΫ»γœ¬Ά≥ΦΤΆΦ±μΘΚ
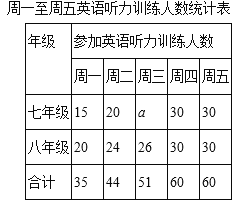

Θ®1Θ©ΧνΩ’ΘΚaΘΫΓΓ ΓΓΘΜ
Θ®2Θ©ΗυΨί…œ ωΆ≥ΦΤΆΦ±μΆξ≥…œ¬±μ÷–ΒΡœύΙΊΆ≥ΦΤΝΩΘΚ
ΡξΦΕ | ΤΫΨυ―ΒΝΖ ±ΦδΒΡ÷–ΈΜ ΐ | ≤ΈΦ””Δ”οΧΐΝΠ―ΒΝΖ»Υ ΐΒΡΖΫ≤ν |
ΤΏΡξΦΕ | 24 | 34 |
ΑΥΡξΦΕ | ΓΓ ΓΓ | 14.4 |
Θ®3Θ©«κΡψάϊ”Ο…œ ωΆ≥ΦΤΆΦ±μΕ‘ΤΏΓΔΑΥΡξΦΕ”Δ”οΧΐΝΠ―ΒΝΖ«ιΩω–¥≥ωΝΫΧθΚœάμΒΡΤάΦέΘΜ
Θ®4Θ©«κΡψΫαΚœ÷ή“Μ÷Ν÷ήΈε”Δ”οΧΐΝΠ―ΒΝΖ»Υ ΐΆ≥ΦΤ±μΘ§ΙάΦΤΗΟ–ΘΤΏΓΔΑΥΡξΦΕΙ≤480Οϊ―ß…ζ÷–÷ή“Μ÷Ν÷ήΈεΤΫΨυΟΩΧλ”–Εύ…Ό»ΥΫχ––”Δ”οΧΐΝΠ―ΒΝΖΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τ“ΜΧθΜΓΨ≠Ιΐ“ΜΗωΕύ±Ώ–ΈœύΝΎΝΫ±Ώ÷–ΒψΘ§≤Δ«“ΗΟΜΓ…œΥυ”–ΒψΕΦ‘ΎΗΟΕύ±Ώ–ΈΒΡΡΎ≤ΩΜρ±Ώ…œΘ§‘ρ≥ΤΗΟΜΓΈΣ¥ΥΝΫ±Ώ÷–ΒψΝ§œΏΒΡEVAΜΓΘ°άΐ»γΘ§ΆΦ1÷–Θ§‘ΎΓςABC÷–Θ§DΘ§EΖ÷±π «ΓςABCΝΫ±ΏΒΡ÷–ΒψΘ§»γΙϊ![]() …œΒΡΥυ”–ΒψΕΦ‘ΎΓςABCΒΡΡΎ≤ΩΜρ±Ώ…œΘ§‘ρ≥Τ
…œΒΡΥυ”–ΒψΕΦ‘ΎΓςABCΒΡΡΎ≤ΩΜρ±Ώ…œΘ§‘ρ≥Τ![]() ΈΣDEΒΡ“ΜΧθEVAΜΓΘ°
ΈΣDEΒΡ“ΜΧθEVAΜΓΘ°
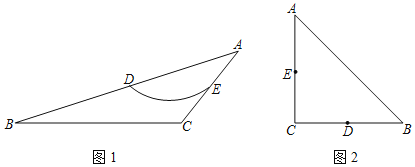
Θ®1Θ©»γΆΦ2Θ§‘ΎRtΓςABC÷–Θ§ΓœCΘΫ90ΓψΘ§ACΘΫBCΘΫ4![]() Θ§DΘ§EΖ÷±π «BCΘ§ACΒΡ÷–ΒψΘ§Μ≠≥ωDEΒΡΉν≥ΛΒΡEVAΜΓ
Θ§DΘ§EΖ÷±π «BCΘ§ACΒΡ÷–ΒψΘ§Μ≠≥ωDEΒΡΉν≥ΛΒΡEVAΜΓ![]() Θ§≤Δ÷±Ϋ”–¥≥ω¥Υ ±
Θ§≤Δ÷±Ϋ”–¥≥ω¥Υ ±![]() ΒΡ≥ΛΘΜ
ΒΡ≥ΛΘΜ
Θ®2Θ©‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷ΣΒψAΘ®0Θ§4Θ©Θ§BΘ®0Θ§0Θ©Θ§CΘ®4tΘ§0Θ©Θ®tΘΨ0Θ©Θ§‘ΎΓςABC÷–Θ§DΘ§EΖ÷±π «ABΘ§ACΒΡ÷–ΒψΘ°
ΔΌ»τtΘΫ1Θ§«σDEΒΡEVAΜΓ![]() Υυ‘Ύ‘≤ΒΡ‘≤–ΡPΒΡΉίΉχ±ξmΒΡ»Γ÷ΒΖΕΈßΘΜ
Υυ‘Ύ‘≤ΒΡ‘≤–ΡPΒΡΉίΉχ±ξmΒΡ»Γ÷ΒΖΕΈßΘΜ
ΔΎ»τ‘ΎΓςABC÷–¥φ‘Ύ“ΜΧθDEΒΡEVAΜΓ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() Υυ‘Ύ‘≤ΒΡ‘≤–ΡP‘ΎΓςABCΒΡΡΎ≤ΩΜρ±Ώ…œΘ§÷±Ϋ”–¥≥ωtΒΡ»Γ÷ΒΖΕΈßΘ°
Υυ‘Ύ‘≤ΒΡ‘≤–ΡP‘ΎΓςABCΒΡΡΎ≤ΩΜρ±Ώ…œΘ§÷±Ϋ”–¥≥ωtΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ“ΜΗω≤ΜΆΗΟςΒΡ≤Φ¥ϋάοΉΑ”–4Ηω±ξΚ≈ΈΣ1ΓΔ2ΓΔ3ΓΔ4ΒΡ–Γ«ρΘ§ΥϋΟ«ΒΡ≤Ρ÷ ΓΔ–ΈΉ¥ΓΔ¥σ–ΓΆξ»ΪœύΆ§Θ§–ΓΝΝ¥”≤Φ¥ϋάοΥφΜζΟΰ≥ω“ΜΗω–Γ«ρΘ§Φ«œ¬ ΐΉ÷ΈΣxΘ§–ΓΗ’¥” Θœ¬ΒΡ3Ηω–Γ«ρ÷–ΥφΜζΟΰ≥ω“ΜΗω–Γ«ρΘ§Φ«œ¬ ΐΉ÷ΈΣyΘ§’β―υ»ΖΕ®ΝΥΒψPΒΡΉχ±ξΘ®xΘ§yΘ©Θ°
Θ®1Θ©»τ–ΓΝΝΟΰ≥ωΒΡ–Γ«ρ…œΒΡ ΐΉ÷ «2Θ§Ρ«Ο¥–ΓΗ’Οΰ≥ωΒΡ–Γ«ρ…œΒΡ ΐΉ÷ «4ΒΡΗ≈¬ «Εύ…ΌΘΩ
Θ®2Θ©άϊ”ΟΜ≠ ςΉ¥ΆΦΜρΝ–±μΗώΒΡΖΫΖ®Θ§«σΒψPΘ®xΘ§yΘ©‘ΎΚ· ΐyΘΫ©¹x+6ΒΡΆΦœσ…œΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
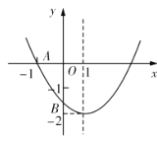
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΕΰ¥ΈΚ· ΐ![]()
![]() ΒΡΆΦœώ”κ
ΒΡΆΦœώ”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§”κ
Θ§”κ![]() ÷αΒΡΫΜΒψ
÷αΒΡΫΜΒψ![]() ‘Ύ
‘Ύ![]() ΚΆ
ΚΆ![]() ÷°ΦδΘ®≤ΜΑϋά®’βΝΫΒψΘ©Θ§Ε‘≥Τ÷αΈΣ÷±œΏ
÷°ΦδΘ®≤ΜΑϋά®’βΝΫΒψΘ©Θ§Ε‘≥Τ÷αΈΣ÷±œΏ![]() .œ¬Ν–Ϋα¬έΘΚ
.œ¬Ν–Ϋα¬έΘΚ
ΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() ΘΜΔέ
ΘΜΔέ![]() ΘΜΔή
ΘΜΔή![]() ΘΜΔί
ΘΜΔί![]() .
.
Τδ÷–’ΐ»ΖΫα¬έ”– __________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com