Question

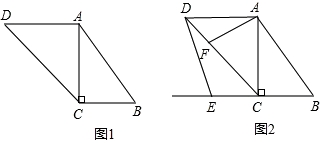
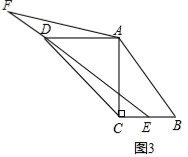
如图1，在梯形ABCD中，AD∥BC，对角线AC⊥BC，AD=8cm，∠D=45°，BC=6cm．

（1）求cos∠B的值；

（2）点E为BC延长线上的动点，点F在线段CD上（点F与点C不重合），且满足∠AFC=∠ADE，如图2，设BE=x，DF=y，求y关于x的函数解析式，并写出函数的定义域；

（3）点E为射线BC上的动点，点F在射线CD上，仍然满足∠AFC=∠ADE，当△AFD的面积为3cm²时，求BE的长．

Answer 1

【考点】相似形综合题．

【分析】（1）要求cos∠B的值，由条件知道△ACB是直角三角形，然后 根据余弦定义就可以求出．

（2）要求函数的解析式，需要运用∠AFC=∠ADE 寻找相似三角形，利用线段比来代换y与x之间的关系，找三角形相似是关键．

（3）要求BE的长，点E存在两种情况，再运用（2）的相似结论，根据相似三角形的面积比得关系就可以求出BE的长．

【解答】解：（1）∵AD∥BC，

∴∠ACB=∠DAC．

∵AC⊥BC，

∴∠ACB=90°．

∴∠DAC=90°．

∵∠D=45°，

∴∠ACD=45°．

∴AD=AC．

∵AD=8cm，

∴AC=8cm．

∵BC=6cm，

∴AB=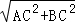=10cm．

∴cos∠B==．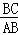

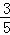（2）∵AD∥BC，

∴∠ADF=∠DCE．     

∵∠AFC=∠FDA+∠FAD，∠ADE=∠FDA+∠EDC，

又∵∠AFC=∠ADE，

∴∠FAD=∠EDC．

∴△ADF∽△DCE．

∴=．

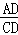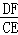在Rt△ADC中，DC²=AD²+AC²，

∵AD=AC=8cm，

∴DC=8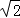cm．

∵BE=xcm，

∴CE=（x﹣6）cm．

又∵DF=ycm，

∴=．

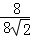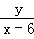∴y=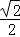x﹣3．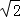

定义域为6＜x＜22．

（3）当点E在BC的延长线上，由（2）可得：△ADF∽△DCE，

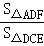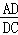∴=（）²，

∵S_△AFD=3cm²，AD=8cm，DC=8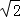cm，

∴S_△DCE=6cm²．

∵S_△DCE=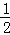×CE×AC，

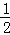∴×（BE﹣6）×8=6，

∴BE=7.5cm．

如图3，当点E在线段BC上，

由（2）△ADF∽△DCE，

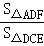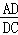∴=（）²，

∵S_△AFD=3cm²，AD=8cm，DC=8cm，

∴S_△DCE=6cm²．

∴S_△DCE=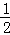×（6﹣BE）×8=6．

∴BE=4.5cm．

所以BE的长为7.5cm或4.5cm．