
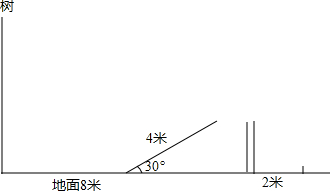
 树照在地面影子长8米,照在斜坡上4米,已知斜坡角度30度,同一时刻将1米木棍竖直在地面上,影子长2米,求:树高.
树照在地面影子长8米,照在斜坡上4米,已知斜坡角度30度,同一时刻将1米木棍竖直在地面上,影子长2米,求:树高. 分析 根据题意画出树的影子,进而利用勾股定理以及平行投影的性质得出树的影长,进而求出即可.
解答 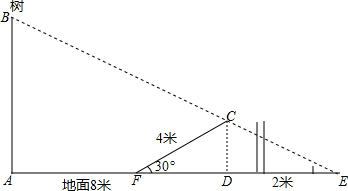 解:如图所示:连接BC并延长到AF延长线上于一点E,
解:如图所示:连接BC并延长到AF延长线上于一点E,
过点C作CD⊥EF于点D,
∵∠CFD=30°,AC=4m,
∴DC=2m,
∴DF=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$(m),
∵同一时刻将1米木棍竖直在地面上,影子长2米,
∴DE=4m,
∴AE=8+2$\sqrt{3}$+4=(12+2$\sqrt{3}$)m,
∴AB=$\frac{1}{2}$(12+2$\sqrt{3}$)=(6+$\sqrt{3}$)m.
答:树高为(6+$\sqrt{3}$)m.
点评 此题主要考查了平行投影以及勾股定理等知识,得出DF,DE的长是解题关键.


 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:选择题
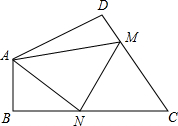 如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )
如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )| A. | 90° | B. | 100° | C. | 130° | D. | 140° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(2a-3b)(3b-2a) | B. | (2a-3b)(3a+2b) | C. | (2a+3b)(-2a-3b) | D. | (2a+3b)(3b-2a) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com