
【题目】在探索三角形全等的条件时,老师给出了定长线段a,b,且长度为b的边所对的角为n°(0<n<90°)小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中AB=a,BD=BC=b,发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:
(1)当n=45时(如图2),小明测得∠ABC=65°,请根据小明的测量结果,求∠ABD的大小;
(2)当n≠45时,将△ABD沿AB翻折,得到△ABD′(如图3),小明和小亮发现∠D′BC的大小与角度n有关,请找出它们的关系,并说明理由;
(3)如图4,在(2)问的基础上,过点B作AD′的垂线,垂足为点E,延长AE到点F,使得EF=![]() (AD+AC),连接BF,请判断△ABF的形状,并说明理由.
(AD+AC),连接BF,请判断△ABF的形状,并说明理由.

【答案】(1)25°;(2)∠D'BC=180°﹣2n°,证明见解析;(3)等腰三角形,证明见解析.
【解析】
(1)先根据三角形的内角和得∠C=70°,由等腰三角形的性质得∠BDC=70°,从而得∠CBD的度数,可得结论;(2)设∠BDC=∠C=α,根据三角形的内角和与三角形外角的性质分别表示∠ABD和∠DBC,相加可得结论;(3)作垂线BT,根据角平分线的性质得:BE=BT,证明Rt△ABE≌Rt△ABT(HL),得AE=AT,证明BE是AF的垂直平分线,可得结论.
解:(1)如图2,△ABC中,∠A=n°=45°,∠ABC=65°,
∴∠C=180°﹣45°﹣65°=70°,
∵BD=BC,
∴∠BDC=∠C=70°,
∴∠DBC=180°﹣2×70°=40°,
∴∠ABD=65°﹣40°=25°;
(2)如图3,∠D'BC=180°﹣2n°,理由是:
设∠BDC=∠C=α,
∴∠DBC=180°﹣2α,
△ADB中,∠BDC=∠DAB+∠ABD,
即α=n°+∠ABD,
∴∠ABD=α﹣n°,
由翻折得:∠ABD'=∠ABD=α﹣n°,
∴∠D'BC=∠D'BD+∠DBC=2∠ABD+∠DBC=2(α﹣n°)+(180°﹣2α)=180°﹣2n°;
(3)△ABF是等腰三角形,且BF=AB,理由是:
如图4,过B作BT⊥AC于T,
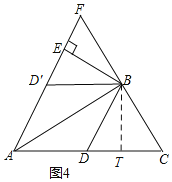
由折叠得:∠D'BC=∠DAB,
∵BE⊥AF,
∴BE=BT,
在Rt△ABE和Rt△ABT中,![]() ,
,
∴Rt△ABE≌Rt△ABT(HL),
∴AE=AT,
∵AD=AD',
∴DT=D'E=TC,
∴![]() =AT,
=AT,
∵EF=![]() ,
,
∴AT=EF=AE,
∵BE⊥AF,即BE是AF的垂直平分线,
∴BF=AB,
∴△ABF是等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ ABC 和△ADE都是等边三角形,点 B 在 ED 的延长线上.
(1)求证:△ABD≌△ACE.
(2)求证:AE+CE=BE.
(3)求∠BEC 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的是速度都为1厘米/秒.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(秒).

(1)当运动时间为t秒时,BQ的长为_____厘米,BP的长为______厘米.(用含t的式子表示)
(2)当t为何值时,△PBQ是直角三角形.
(3)如图2,连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC边上的高AG平分∠BAC.
(1)如图1,求证:AB=AC.
(2)如图2,点D、E在△ABC的边BC上,AD=AE,BC=10cm,DE=6cm,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )

A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣![]() x﹣1交于点C.
x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣![]() x﹣1交于点C.
x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com