
【题目】如图,已知A(﹣2,0),B(4,0),抛物线y=ax2+bx﹣1过A、B两点,并与过A点的直线y=﹣![]() x﹣1交于点C.
x﹣1交于点C.
(1)求抛物线解析式及对称轴;
(2)在抛物线的对称轴上是否存在一点P,使四边形ACPO的周长最小?若存在,求出点P的坐标,若不存在,请说明理由;
(3)点M为y轴右侧抛物线上一点,过点M作直线AC的垂线,垂足为N.问:是否存在这样的点N,使以点M、N、C为顶点的三角形与△AOC相似,若存在,求出点N的坐标,若不存在,请说明理由.

【答案】(1)抛物线解析式为:y=![]() ,抛物线对称轴为直线x=1;(2)存在P点坐标为(1,﹣
,抛物线对称轴为直线x=1;(2)存在P点坐标为(1,﹣![]() );(3)N点坐标为(4,﹣3)或(2,﹣1)
);(3)N点坐标为(4,﹣3)或(2,﹣1)
【解析】(1)由待定系数法求解即可;
(2)将四边形周长最小转化为PC+PO最小即可;
(3)利用相似三角形对应点进行分类讨论,构造图形.设出点N坐标,表示点M坐标代入抛物线解析式即可.
(1)把A(-2,0),B(4,0)代入抛物线y=ax2+bx-1,得
![]()
解得
∴抛物线解析式为:y=![]() x2
x2![]() x1
x1
∴抛物线对称轴为直线x=-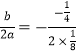 =1
=1
(2)存在
使四边形ACPO的周长最小,只需PC+PO最小
∴取点C(0,-1)关于直线x=1的对称点C′(2,-1),连C′O与直线x=1的交点即为P点.
设过点C′、O直线解析式为:y=kx
∴k=-![]()
∴y=-![]() x
x
则P点坐标为(1,-![]() )
)
(3)当△AOC∽△MNC时,
如图,延长MN交y轴于点D,过点N作NE⊥y轴于点E
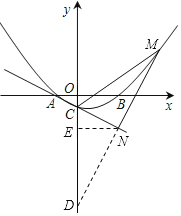
∵∠ACO=∠NCD,∠AOC=∠CND=90°
∴∠CDN=∠CAO
由相似,∠CAO=∠CMN
∴∠CDN=∠CMN
∵MN⊥AC
∴M、D关于AN对称,则N为DM中点
设点N坐标为(a,-![]() a-1)
a-1)
由△EDN∽△OAC
∴ED=2a
∴点D坐标为(0,-![]() a1)
a1)
∵N为DM中点
∴点M坐标为(2a,![]() a1)
a1)
把M代入y=![]() x2
x2![]() x1,解得
x1,解得
a=4
则N点坐标为(4,-3)
当△AOC∽△CNM时,∠CAO=∠NCM
∴CM∥AB则点C关于直线x=1的对称点C′即为点N
由(2)N(2,-1)
∴N点坐标为(4,-3)或(2,-1)


科目:初中数学 来源: 题型:
【题目】如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
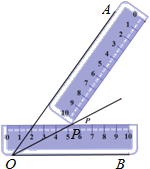
A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边的距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探索三角形全等的条件时,老师给出了定长线段a,b,且长度为b的边所对的角为n°(0<n<90°)小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中AB=a,BD=BC=b,发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:
(1)当n=45时(如图2),小明测得∠ABC=65°,请根据小明的测量结果,求∠ABD的大小;
(2)当n≠45时,将△ABD沿AB翻折,得到△ABD′(如图3),小明和小亮发现∠D′BC的大小与角度n有关,请找出它们的关系,并说明理由;
(3)如图4,在(2)问的基础上,过点B作AD′的垂线,垂足为点E,延长AE到点F,使得EF=![]() (AD+AC),连接BF,请判断△ABF的形状,并说明理由.
(AD+AC),连接BF,请判断△ABF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只蚂蚁在网格(每小格边长为1)上沿着网格线运动.它从格点![]() 处出发去看望格点B、C、D等处的蚂蚁,规定:向上向右走均为正,向下向左走均为负.如:从A到B记为:
处出发去看望格点B、C、D等处的蚂蚁,规定:向上向右走均为正,向下向左走均为负.如:从A到B记为:![]() ,从B到A记为:
,从B到A记为:![]() ,其中第一个数表示左右方向,第二个数表示上下方向.
,其中第一个数表示左右方向,第二个数表示上下方向.

(1)填空:图中![]() ,
,![]() ;
;
(2)若这只蚂蚁从A处去M处的蚂蚁的行走路线依次为![]() ,
,![]() ,
,![]() ,
,![]() ,则点M的坐标为(________,________);
,则点M的坐标为(________,________);
(3)若图中另有两个格点Р、Q,且![]() ,
,![]() ,则从Q到A记为________________.
,则从Q到A记为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长
(2)若E是边AB上的动点,求线段DE的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C'处,BC'交AD于点E.

(1)试判断△BDE的形状,并说明理由;
(2)若AB=6,AD=8,求△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于P,Q两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)证明AP=AQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验中学为了了解今年参加中招考试九年级300名学生的体育成绩,特对学生参加课外锻炼的情况进行了摸底,随机对九年级30名学生一周内平均每天参加课外锻炼的时间进行了调查,结果如下:(单位:分钟)

(1)补全频数分布表和频数分布直方图.

(2)填空:在这个问题中,总体是___________,样本是_________.
由统计分析得,这组数据的平均数是39.37(分),众数是______,中位数是______.
(3)如果描述该校300名学生一周内平均每天参加课外锻炼时间的总体情况,你认为用平均数、众数、中位数中的哪一个量比较合适?
(4)估计实验中学九年级有多少名学生,平均每天参加课外锻炼的时间多于30分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com