
【题目】如图1,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的是速度都为1厘米/秒.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(秒).

(1)当运动时间为t秒时,BQ的长为_____厘米,BP的长为______厘米.(用含t的式子表示)
(2)当t为何值时,△PBQ是直角三角形.
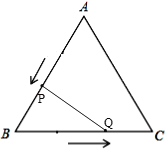
(3)如图2,连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
【答案】(1)t,5﹣t;(2)第![]() 秒或第
秒或第![]() 秒;(3)不变,∠CMQ=60°.
秒;(3)不变,∠CMQ=60°.
【解析】
(1)根据距离=速度×时间,结合图形解答即可;(2)分∠PQB=90°、∠BPQ=90°两种情况,根据含30°角的直角三角形的性质列式计算即可;(3)利用SAS证明△ABQ≌△CAP,可得∠BAQ=∠ACP,根据三角形外角性质及等边三角形的内角是60°解答即可.
(1)∵点P、Q的速度都为1厘米/秒.
∴BQ=t,AP=t,
∴BP=5-t,
故答案为:t,(5﹣t)
(2)设时间为t,则AP=BQ=t,PB=5﹣t,
①如图,当∠PQB=90°时,
∵∠B=60°,
∴∠BPQ=30°,
∴PB=2BQ,得5﹣t=2t,
解得,t=![]() ,
,
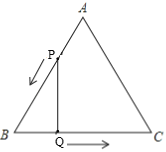
②如图,当∠BPQ=90°时,
∵∠B=60°,
∴∠BQP=30°,
∴BQ=2BP,得t=2(5﹣t),
解得,t=![]() ,
,
∴当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形;
秒时,△PBQ为直角三角形;
(3)∠CMQ不变,理由如下:
在△ABQ与△CAP中, ,
,
∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°,
∴∠CMQ不会变化.


科目:初中数学 来源: 题型:
【题目】已知直线y=2x-7平移后的图象l经过点(-3,-2),
(1)求l的函数解析式;并画出该函数的图象;
(2)l与x轴交于点A,点P是l上一点,且S△AOP=![]() ,求点P的坐标.
,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣![]() <0的x的取值范围;
<0的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
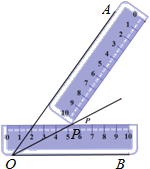
A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边的距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为53°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度i=5:12.
(1)求此人所在位置点P的铅直高度.(结果精确到0.1米)
(2)求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)
(测倾器的高度忽略不计,参考数据:tan53°≈![]() ,tan63.5°≈2)
,tan63.5°≈2)

查看答案和解析>>
科目:初中数学 来源: 题型:
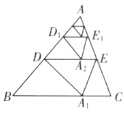
【题目】如图,将![]() 沿着过
沿着过![]() 中点D的直线折叠,使点A落在
中点D的直线折叠,使点A落在![]() 边上的
边上的![]() 处,称为第1次操作,折痕
处,称为第1次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,还原纸片后,再将
,还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点A落在
的直线折叠,使点A落在![]() 边上的
边上的![]() 处,称为笫2次操作,折痕
处,称为笫2次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() .按上述方法不断操作下去……经过第2015次操作后得到的折痕
.按上述方法不断操作下去……经过第2015次操作后得到的折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1), 已知△ABC中, ∠BAC=900, AB=AC, AE是过A的一条直线, 且B、C在A、E的异侧, BD⊥AE于D, CE⊥AE于E

(1)试说明: BD=DE+CE.
(2)若直线AE绕A点旋转到图(2)位置时(BD<CE), 其余条件不变, 问BD与DE、CE的关系如何? 为什么?

(3)若直线AE绕A点旋转到图(3)位置时(BD>CE), 其余条件不变, 问BD与DE、CE的关系如何? 请 直接写出结果, 不需说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探索三角形全等的条件时,老师给出了定长线段a,b,且长度为b的边所对的角为n°(0<n<90°)小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中AB=a,BD=BC=b,发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:
(1)当n=45时(如图2),小明测得∠ABC=65°,请根据小明的测量结果,求∠ABD的大小;
(2)当n≠45时,将△ABD沿AB翻折,得到△ABD′(如图3),小明和小亮发现∠D′BC的大小与角度n有关,请找出它们的关系,并说明理由;
(3)如图4,在(2)问的基础上,过点B作AD′的垂线,垂足为点E,延长AE到点F,使得EF=![]() (AD+AC),连接BF,请判断△ABF的形状,并说明理由.
(AD+AC),连接BF,请判断△ABF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C'处,BC'交AD于点E.

(1)试判断△BDE的形状,并说明理由;
(2)若AB=6,AD=8,求△BDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com