
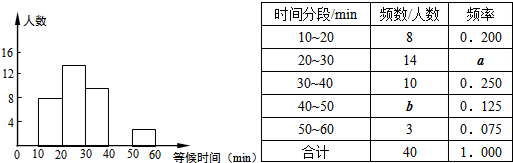
 解:(1)填抽样调查或抽查;总人数为:8÷0.200=40;
解:(1)填抽样调查或抽查;总人数为:8÷0.200=40;

科目:初中数学 来源: 题型:
 一楼房AB后有一假山,其坡面CE与水平地面的夹角为30°,在阳光的照射下,楼房AB落在地上的影长为BC=25米,落在坡面的影长为CE=20米,已知小丽测得同一时刻1米高的竹竿在水平面上的影长为0.8米,求楼房AB的高度.
一楼房AB后有一假山,其坡面CE与水平地面的夹角为30°,在阳光的照射下,楼房AB落在地上的影长为BC=25米,落在坡面的影长为CE=20米,已知小丽测得同一时刻1米高的竹竿在水平面上的影长为0.8米,求楼房AB的高度.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,∠MAN=45°,B、C为AN上的两点,且AB=BC=2,D为射线AN上的一个动点,过B、C、D三点作⊙O,则sin∠BDC的最大值为( )
如图,∠MAN=45°,B、C为AN上的两点,且AB=BC=2,D为射线AN上的一个动点,过B、C、D三点作⊙O,则sin∠BDC的最大值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴为x=-1,与x轴交于点A,B(1,0),与y轴交于点C,则下列四个结论:①abc<0;②4a-2b+c>0;③2a+b=0;④当y<0时,x<-3或x>1.其中正确的个数是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴为x=-1,与x轴交于点A,B(1,0),与y轴交于点C,则下列四个结论:①abc<0;②4a-2b+c>0;③2a+b=0;④当y<0时,x<-3或x>1.其中正确的个数是( )| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)如图是2×2的方格(每个小正方格的边长为1个单位长度),先在方格内画出面积为2平方单位的正方形(用阴影部分表示),再用圆规在所给图的数轴上准确地表示实数
(1)如图是2×2的方格(每个小正方格的边长为1个单位长度),先在方格内画出面积为2平方单位的正方形(用阴影部分表示),再用圆规在所给图的数轴上准确地表示实数| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com