
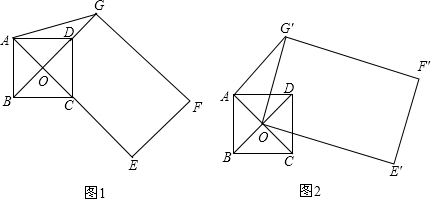
���� ��1���ȸ�����ת�����ʵá�DOG��=����OG=OG��=OA��Ȼ�����ú�30�ȵ�ֱ�����������ߵĹ�ϵ�����AG��O��Ȼ������DOG��Ķ������ɣ�ͬ���ɵæ��Ķ���Ϊ150�㣻
��2������AF�䡢OF�䣬��ͼ1�����������ε����ʼ����OA=OD=OC����ɵõ�OG���OE��ij������ù��ɶ��������OF�䣬�������������ߵĹ�ϵ�õ�OA+OF���AF�䣨����F��AO���ӳ�����ȡ�Ⱥţ������ǿɵõ�AF������ֵ��
��� �⣺��1�����ı���ABCDΪ�����Σ�
��OA=OD����AOD=90�㣬
��OG=2OD��
��OG=2OA��
�߾���OEFG�Ƶ�O��ʱ����ת���ǣ�0�㣼����360�㣩�õ�������OE��F��G�䣬
���DOG��=����OG=OG��=2OA��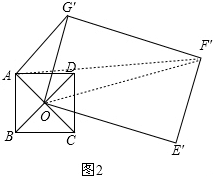
����OAG��=90�㣬
��OA=$\frac{1}{2}$OG�䣬
���AG��O=30�㣬
���AOG��=60�㣬
���DOG��=90��-60��=30�㣬
�����Ķ���Ϊ30�㣻
ͬ���ɵæ��Ķ���Ϊ150�㣻
����Ķ���Ϊ30���150�㣻
��2������AF��OF����ͼ2��
��������ABCD�ı߳�Ϊ1��
��OA=OD=OC=$\frac{\sqrt{2}}{2}$��
��OG��=2OD=$\sqrt{2}$��OE��=3OC=$\frac{3\sqrt{2}}{2}$��
���ı���OG��F��E��Ϊ���Σ�
��E��F��=OG=$\sqrt{2}$����E��=90�㣬
��Rt��OE��F����OF��=$\sqrt{��\sqrt{2}��^{2}+��\frac{3\sqrt{2}}{2}��^{2}}$=$\frac{\sqrt{26}}{2}$��
��OA+OF���AF�䣨����F����AO���ӳ�����ȡ�Ⱥţ���
��AF������ֵ=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{26}}{2}$=$\frac{\sqrt{2}+\sqrt{26}}{2}$��
���� ���⿼������ת�����ʣ���Ӧ�㵽��ת���ĵľ�����ȣ���Ӧ������ת���������߶εļнǵ�����ת�ǣ���תǰ�����ͼ��ȫ�ȣ�Ҳ�����������ε����ʣ������2��С��Ĺؼ��������������ߵĹ�ϵ�жϵ�F����AO���ӳ���ʱAF�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
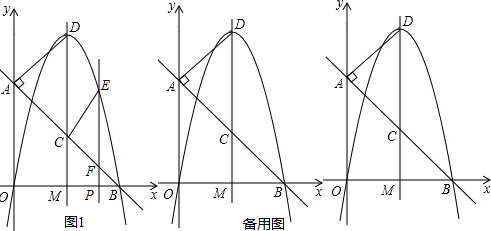
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B�� | 5$\sqrt{5}$-2$\sqrt{2}$=3$\sqrt{3}$ | C�� | 2$\sqrt{3}$��$3\sqrt{3}$=6$\sqrt{3}$ | D�� | $\sqrt{2}$$��\sqrt{3}$=$\frac{\sqrt{6}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4.659��105 | B�� | 4.659��104 | C�� | 0.4659��105 | D�� | 46.6��103 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 45�� | C�� | 60�� | D�� | 90�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com