
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 为
为![]() 上两点,且
上两点,且![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.

(1)如图1,当![]() 两点重合时,求证:
两点重合时,求证:![]() ;
;
(2)延长![]() 与
与![]() 交于点
交于点![]() .
.
①如图2,求证:![]() ;
;
②如图3,连接![]() ,若
,若![]() ,则
,则![]() 的面积为______________.
的面积为______________.
【答案】(1)见解析;(2)①见解析;②2.
【解析】
(1)当D、E两点重合时,则AD=CD,然后由等边三角形的性质可得∠CBD的度数,根据等腰三角形的性质和三角形的外角性质可得∠F的度数,于是可得∠CBD与∠F的关系,进而可得结论;
(2)①过点E作EH∥BC交AB于点H,连接BE,如图4,则易得△AHE是等边三角形,根据等边三角形的性质和已知条件可得EH=CF,∠BHE=∠ECF=120°,BH=EC,于是可根据SAS证明△BHE≌△ECF,可得∠EBH=∠FEC,易证△BAE≌△BCD,可得∠ABE=∠CBD,从而有∠FEC=∠CBD,然后根据三角形的内角和定理可得∠BGE=∠BCD,进而可得结论;
②易得∠BEG=90°,于是可知△BEF是等腰直角三角形,由30°角的直角三角形的性质和等腰直角三角形的性质易求得BE和BF的长,过点E作EM⊥BF于点F,过点C作CN⊥EF于点N,如图5,则△BEM、△EMF和△CFN都是等腰直角三角形,然后利用等腰直角三角形的性质和30°角的直角三角形的性质可依次求出BM、MC、CF、FN、CN、GN的长,进而可得△GCN也是等腰直角三角形,于是有∠BCG=90°,故所求的△BCG的面积=![]() ,而BC和CG可得,问题即得解决.
,而BC和CG可得,问题即得解决.
解:(1)∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,
当D、E两点重合时,则AD=CD,∴![]() ,
,
∵![]() ,∴∠F=∠CDF,
,∴∠F=∠CDF,
∵∠F+∠CDF=∠ACB=60°,∴∠F=30°,
∴∠CBD=∠F,∴![]() ;
;
(2)①∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,AB=AC,
过点E作EH∥BC交AB于点H,连接BE,如图4,则∠AHE=∠ABC=60°,∠AEH=∠ACB=60°,
∴△AHE是等边三角形,∴AH=AE=HE,∴BH=EC,
∵![]() ,CD=CF,∴EH=CF,
,CD=CF,∴EH=CF,
又∵∠BHE=∠ECF=120°,∴△BHE≌△ECF(SAS),
∴∠EBH=∠FEC,EB=EF,
∵BA=BC,∠A=∠ACB=60°,AE=CD,
∴△BAE≌△BCD(SAS),∴∠ABE=∠CBD,∴∠FEC=∠CBD,
∵∠EDG=∠BDC,∴∠BGE=∠BCD=60°;

②∵∠BGE=60°,∠EBD=30°,∴∠BEG=90°,
∵EB=EF,∴∠F=∠EBF=45°,
∵∠EBG=30°,BG=4,∴EG=2,BE=2![]() ,
,
∴BF=![]() ,
,![]() ,
,
过点E作EM⊥BF于点F,过点C作CN⊥EF于点N,如图5,则△BEM、△EMF和△CFN都是等腰直角三角形,
∴![]() ,
,
∵∠ACB=60°,∴∠MEC=30°,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,∴∠GCF=90°=∠GCB,
,∴∠GCF=90°=∠GCB,
∴![]() ,
,
∴△BCG的面积=![]() .
.
故答案为:2.



科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,直线
,直线![]() 经过点
经过点![]() 和
和![]() .
.

(1)![]() 点的坐标为( , ),
点的坐标为( , ),![]() 点的坐标为( , );
点的坐标为( , );
(2)如图1,已知直线![]() 经过点
经过点![]() 和
和![]() 轴上一点
轴上一点![]() ,
,![]() ,点
,点![]() 在直线AB上且位于
在直线AB上且位于![]() 轴右侧图象上一点,连接
轴右侧图象上一点,连接![]() ,且
,且![]()
![]() .
.
①求![]() 点坐标;
点坐标;
②将![]() 沿直线AM 平移得到
沿直线AM 平移得到![]() ,平移后的点
,平移后的点![]() 与点
与点![]() 重合,
重合,![]() 为
为![]() 上的一动点,当
上的一动点,当![]() 的值最小时,请求出最小值及此时 N 点的坐标;
的值最小时,请求出最小值及此时 N 点的坐标;
(3)如图 2,将点![]() 向左平移 2 个单位到点
向左平移 2 个单位到点![]() ,直线
,直线![]() 经过点
经过点![]() 和
和![]() ,点
,点![]() 是点
是点![]() 关于
关于![]() 轴的对称点,直线
轴的对称点,直线![]() 经过点
经过点![]() 和点
和点![]() ,动点
,动点![]() 从原点出发沿着
从原点出发沿着![]() 轴正方向运动,连接
轴正方向运动,连接![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,求出
是等腰直角三角形?若存在,求出![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,![]() 、
、![]() ,且
,且![]() 、
、![]() 满足
满足![]()
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
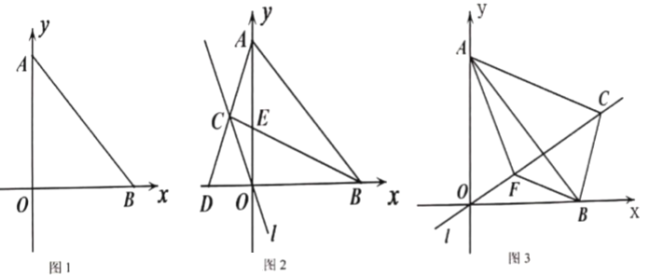
(2)过点![]() 的直线
的直线![]() 上有一点
上有一点![]() ,连接
,连接![]() 、
、![]() ,
,![]() ,如图2,当点
,如图2,当点![]() 在第二象限时,
在第二象限时,![]() 交
交![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的长为
的长为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
(3)在(2)的条件下,如图3,当点![]() 在第一象限时,过点
在第一象限时,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(![]() )将
)将![]() 化成
化成![]() 的形式.
的形式.
(![]() )与
)与![]() 轴的交点坐标是__________,与
轴的交点坐标是__________,与![]() 轴的交点坐标是__________.
轴的交点坐标是__________.
(![]() )在坐标系中利用描点法画出此抛物线.
)在坐标系中利用描点法画出此抛物线.
|
|
| |||||
|
|
|
(![]() )不等式
)不等式![]() 的解集是__________.
的解集是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“军运会”期间,某纪念品店老板用5000元购进一批纪念品,由于深受顾客喜爱,很快售完,老板又用6000元购进同样数目的这种纪念品,但第二次每个进价比第一次每个进价多了2元.
(1)求该纪念品第一次每个进价是多少元?
(2)老板以每个15元的价格销售该纪念品,当第二次纪念品售出![]() 时,出现了滞销,于是决定降价促销,若要使第二次的销售利润不低于900元,剩余的纪念品每个售价至少要多少元?
时,出现了滞销,于是决定降价促销,若要使第二次的销售利润不低于900元,剩余的纪念品每个售价至少要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
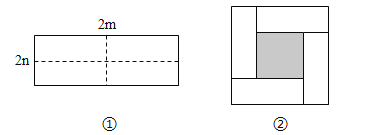
【题目】如图①所示是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成相等个小长方形.然后按图②的方式拼成一个正方形.
的长方形,沿图中虚线用剪刀均分成相等个小长方形.然后按图②的方式拼成一个正方形.
(1)你认为图②中的阴影部分的正方形的边长等于 ;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积:
方法① ;
方法② ;
(3)观察图②,写出![]() ,
,![]() ,
,![]() 这三个代数式之间的等量关系: ;
这三个代数式之间的等量关系: ;
(4)根据(3)题中的等量关系,解决如下问题:若![]() ,
,![]() ,求
,求![]() 的值?
的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
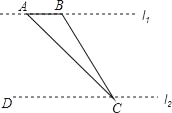
【题目】如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
A. 50m B. 25m C. (50﹣![]() )m D. (50﹣25
)m D. (50﹣25![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;②a﹣b+c<0;③当x<1时,y随x增大而增大;
④抛物线的顶点坐标为(2,b);⑤若ax2+bx+c=b,则b2﹣4ac=0.
其中正确的是( )

A. ①②③ B. ①④⑤ C. ①②④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员的10次射击训练,成绩分别被制成下列两个统计图.
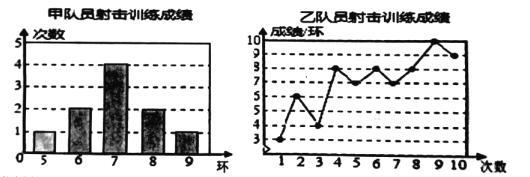
并整理分析数据如下表:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 |
|
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com