
分析 设AD=x,则BC=8-x,列出关于x的二次函数解析式,求出△ABC的面积最大时x的值,根据轴对称的知识确定周长最小时BA+CA的值.
解答 解:设AD=x,则BC=8-x,
△ABC的面积为:y=$\frac{1}{2}$x(8-x)=-$\frac{1}{2}$x2+4x,
根据二次函数的性质,x=4时,面积最大,如图,过点A作BC的平行线l,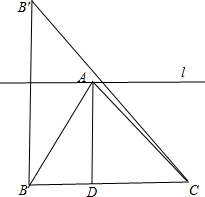
作点关于l的对称点B′
BB′=8,BC=4,
根据勾股定理,CB′=4$\sqrt{5}$,
则△ABC的最小周长为:4$\sqrt{5}$+4.
故答案为:4$\sqrt{5}$+4.
点评 本题考查的是二次函数的最值问题,根据题意列出二次函数的解析式求出最值是解题的关键,注意最短路径问题即轴对称知识的正确运用.


科目:初中数学 来源: 题型:解答题
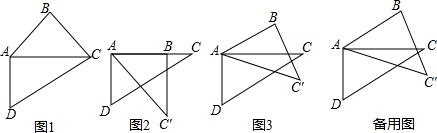
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
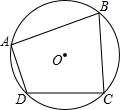 如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )
如图,四边形ABCD是⊙O的内接四边形,若∠B=75°,∠C=85°,则∠D-∠A的度数差为( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=-$\frac{1}{2}$x+4与坐标轴交于A,B两点,C(2,-4),S△PAB=S△ABC,点P在x轴上,求点P的坐标.
如图,直线y=-$\frac{1}{2}$x+4与坐标轴交于A,B两点,C(2,-4),S△PAB=S△ABC,点P在x轴上,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
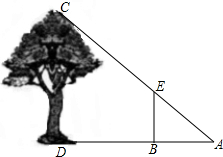 如图,某人在点A处测量树高,点A到树的距离AD为21米,将一长为2米的标杆BE在与点A相距3米的点B处垂直立于地面,此时,观察视线恰好经过标杆顶点E及树的顶点C,求树CD的高.
如图,某人在点A处测量树高,点A到树的距离AD为21米,将一长为2米的标杆BE在与点A相距3米的点B处垂直立于地面,此时,观察视线恰好经过标杆顶点E及树的顶点C,求树CD的高.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com