
����Ŀ����ͼ�٣���֪������C1��y=a��x+1��2��4�Ķ���ΪC����x���ཻ��A��B���㣨��A�ڵ�B����ߣ�����B�ĺ�������1��
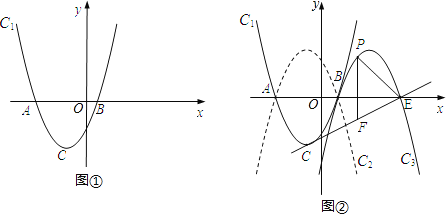
��1�����C�����꼰a ��ֵ��
��2����ͼ�ڣ�������C2��C1����x��Գƣ���������C2����ƽ��4����λ���õ�������C3��C3��x�ύ�ڵ�B��E����P��ֱ��CE�Ϸ�������C3�ϵ�һ�����㣬����P��y���ƽ���ߣ���CE�ڵ�F��
�����߶�PF�������ֵ��
����PE=EF�����P�����꣮
���𰸡���1��a=1������CΪ����1����4������2���ٵ�x=![]() ʱ��PF�����ֵΪ
ʱ��PF�����ֵΪ![]() ����P��
����P��![]() ��
��![]() ����
����
��������
�����������1�����ݶ��κ��������ʼ���ֱ����ö���C�����꣬��B��������뺯������ʽ�������a��ֵ��
��2����C2�Ķ���������C����x��ĶԳƵ㣬�Ҷ�����ϵ����Ϊ�෴�����ݴ˼������C2�Ľ���ʽ��Ȼ�����ƽ�Ƶ��������C3�Ľ���ʽ�����ô���ϵ�������ֱ��CE�Ľ���ʽ����PF�ij���������x��ʾ������Ȼ����ݶ��κ������������PF�����ֵ��
��PE=EF��P��F����x��Գƣ��������껥Ϊ�෴�����ݴ˼����з�����⣮
�⣺��1������CΪ����1����4����
����B��1��0����������C1�ϣ���0=a��1+1��2��4����ã�a=1��
��2������C2��C1����x��Գƣ�
��������C2�ı���ʽΪy=����x+1��2+4��
������C3��C2ƽ�Ƶõ���
��������C3Ϊy=����x��3��2+4=��x2+6x��5��
��E��5��0����
��ֱ��CE�Ľ���ʽΪ��y=kx+b��
��![]() �����
�����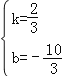 ��
��
��ֱ��BC�Ľ���ʽΪy=![]() x��
x��![]() ��
��
��P��x����x2+6x��5������F��x��![]() x��
x��![]() ����
����
��PF=����x2+6x��5������![]() x��
x��![]() ��=��x2+
��=��x2+![]() x��
x��![]() =����x��
=����x��![]() ��2+
��2+![]() ��
��
����x=![]() ʱ��PF�����ֵΪ
ʱ��PF�����ֵΪ![]() ��
��
����PE=EF����PF��x�ᣬ
��x��ƽ��PF��
����x2+6x��5=��![]() x+
x+![]() ��
��
���x1=![]() ��x2=5����ȥ��
��x2=5����ȥ��
��P��![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AD��BC�ڵ�D��BEƽ����ABC������ABC=64������AEB=70����
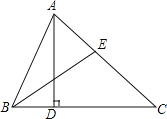
��1������CAD�Ķ�����
��2������FΪ�߶�BC�ϵ�����һ�㣬����EFCΪֱ��������ʱ������BEF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��x�ᡢy��ľ���ֱ���2��3���ҵ�P����y��ԳƵĵ��ڵ������ޣ����P�������� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���÷�֤��֤������һ���������У�������һ���ڽ�С�ڻ����60�㡱Ӧ�ȼ��裺��һ���������У�������
A. ������һ���ڽǴ��ڻ����60�� B. ������һ���ڽǴ���60��
C. ÿһ���ڽ�С�ڻ����60�� D. ÿһ���ڽǴ���60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ԭ���е��Ӻ�ԭ�Ӻ�֮��ľ���Ϊ0.00000000529���ף��ÿ�ѧ��������ʾ�������Ϊ( )
A. 5.29��10��8 cm �� B. 5.29��10��9cm�� C. 0.529��10��8 cm�� D. 52.9��10��10 cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����( ).
A������ֱ�� B����Բ�ǻ�
C��������ȵĻ��ǵȻ� D����Բ�ĵ��߶���ֱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ݵĹ�����д��3��4��5��12��13��84��85��3612��________������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC��һ��P����PA=PB=PC�����Pһ������ABC�� ����
A. ������ƽ���ߵĽ��� B. �������ߵĽ���
C. �����ߵĽ��� D. ���ߴ�ֱƽ���ߵĽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
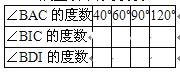
����Ŀ������֪�����κ�һ�������ε������ڽ�ƽ�����ཻ��һ�㣬��ͼ������ABC �������ڽ�ƽ�����ཻ�ڵ�I����I��DE��AI�ֱ�AB��AC�ڵ�D��E��
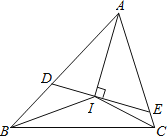
��1������ͨ����ͼ����������д���ϱ���ͼ���ڲݸ�ֽ�ϣ���������ȷ��
��2�����ϱ����㷢������BIC����BDI֮���к�������ϵ����д��������˵�����еĵ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com