
【题目】阅读下列材料解决问题
两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,例如37和82,它们各数位上的数字之和分别为3+7和8+2,显然3+7=8+2=10故37和82互为“调和数”.
(1)下列说法错误的是
A.123和51互为调和数” B.345和513互为“调和数
C.2018和8120互为“调和数” D.两位数![]() 和
和![]() 互为“调和数”
互为“调和数”
(2)若A、B是两个不等的两位数,A=![]() ,B=
,B=![]() ,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A.
,A和B互为“调和数”,且A与B之和是B与A之差的3倍,求满足条件的两位数A.
【答案】(1)B(2)18
【解析】
(1)根据题意,两个多位数整数,若它们各数位上的数字之和相等,则称这两个多位数互为“调和数”,即可作答
(2)先用“调和数”,得出x+y=m+n,再利用A与B之和是B与A之差的3倍,得出10m+n=20x+2y,即可得出m=![]() ,最后利用1≤x≤9,0≤y≤9,计论即可以得出结论
,最后利用1≤x≤9,0≤y≤9,计论即可以得出结论
(1)根据调和数的定义,通过计算各位数之和,易知B选项错误
故答案选B
(2)∵A=![]() ,B=
,B=![]() ,A、B互为“调和数”
,A、B互为“调和数”
∴x+y=m+n①
∵A与B之和是B与A之差的3倍
∴![]()
∴![]()
∴10m+n=20x+2y②
由①②得,m=![]()
∵m为两位数的十位数字
∴1≤m≤9
∴1≤![]() ≤9,
≤9,
∴9≤19x+y≤81,且19x+y是9的倍数
∴19x+y=18或27或36或45或54或63或72或81
则![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]()
∵x,y分别为A的 十位和个位,
∴1≤x≤9,0≤y≤9
∴计算可得,仅当![]() 时满足,此时x=1,y=8,故A为18
时满足,此时x=1,y=8,故A为18
故满足A的值为18


科目:初中数学 来源: 题型:
【题目】我们知道:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.所以式子|x﹣3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,直接下列问题答案:
(1)|5﹣(﹣2)|的值为_____;
(2)若|x﹣3|=1,则x的值为_____;
(3)若|x﹣3|=|x+1|,则x的值为_____;
(4)若|x﹣3|+|x+1|=7,则x的值为_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,王同学使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为![]() ,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )
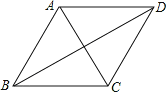
A. △ABD与△ABC的周长相等
B. △ABD与△ABC的面积相等
C. 菱形的周长等于两条对角线之和的两倍
D. 菱形的面积等于两条对角线之积的两倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线(要求:尺规作图,保留作图痕迹,不写作法);
(2)若∠ABC的平分线分别交AD,AC于P,Q两点,证明:AP=AQ.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com