
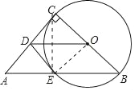
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径作圆,交斜边AB于点E,D为AC的中点.连接DO,DE.则下列结论中不一定正确的是( )
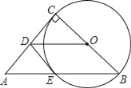
A. DO∥ABB. △ADE是等腰三角形
C. DE⊥ACD. DE是⊙O的切线
【答案】C
【解析】
连接OE,由OD为三角形ABC的中位线,利用中位线定理得到OD与AB平行,选项A正确;由两直线平行得到同位角相等,内错角相等即∠COD=∠B,∠DOE=∠OEB,再由OE=OB,利用等边对等角得到∠OEB=∠B,等量代换得到∠COD=∠DOE,再由OC=OE,OD为公共边得到三角形COD与三角形EOD全等,由全等三角形的对应角相等得到∠OED=∠OCD为直角,即OE垂直于DE,可得出DE为圆O的切线,选项D正确;连接EC,由BC是直径可得∠AEC=∠CEB=90°,在直角三角形AEC中,D为斜边的中点,根据直角三角形斜边上的中线等于斜边的一半可得DE=AD,即三角形AED为等腰三角形,选项B正确,而DE不一定垂直于AC,故选项C符合题意.
连接OE
∵D为AC中点,O为BC中点
∴OD为△ABC的中位线,
∴DO∥AB,选项A正确;
∵∠COD=∠B,∠DOE=∠OEB,
∵OE=OB,
∴∠OEB=∠B,
∴∠COD=∠DOE,
在△COD和△EOD中,
 ,
,
∴△COD≌△EOD(SAS),
∴∠OED=∠OCD=90°,
∴DE为圆O的切线,选项D正确;
连接EC,∵BC是直径,
∴∠AEC=∠CEB=90°,
在RtAEC中,
∵AD=DC,
∴DE=AD,
∴△AED为等腰三角形,选项B正确,
则不一定正确的为DE⊥AC.
故选:C.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A. ![]() B. 2
B. 2![]() -
-![]() C. 2
C. 2![]() -
-![]() D. 4
D. 4![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了开展阳光体育运动,某市教体局做了一个随机调查,调查内容是:每天锻炼是否超过1h及锻炼未超过1h的原因.他们随机调查了600名学生,用所得的数据制成了扇形统计图和频数分布直方图(图1、图2).

根据图示,请回答以下问题:
(1)“没时间”的人数是 ,并补全频数分布直方图;
(2)2016年该市中小学生约40万人,按此调查,可以估计2016年全市中小学生每天锻炼超过1h的约有 万人;
(3)在(2)的条件下,如果计划2018年该市中小学生每天锻炼未超过1h的人数降到7.5万人,求2016年至2018年锻炼未超过1h人数的年平均降低的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某五金商店准备从机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用900元正好可以购进50个甲种零件和50个乙种零件.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出该五金商店本次从机械厂购进甲、乙两种零件有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直径,C为
为直径,C为![]() 上一点.
上一点.
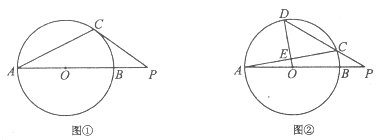
(Ⅰ)如图①,过点C作![]() 的切线,与
的切线,与![]() 的延长线相交于点P,若
的延长线相交于点P,若![]() ,求
,求![]() 的大小;
的大小;
(Ⅱ)如图②,D为弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点E,连接
于点E,连接![]() 并延长,与
并延长,与![]() 的延长线相交于点P,若
的延长线相交于点P,若![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com