
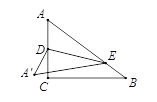
【题目】如图,在△ABC中,∠C=90°,AB=5,BC=4. 点D是边AC的中点,点E在边AB上,将△ADE沿DE翻折,使点A落在点A′处,当线段AE的长为_______时,A′E∥BC.
【答案】![]() 或
或![]()
【解析】
根据∠C=90°,AB=5,BC=4,可得AC=3,由翻折的性质可得△ADE≌△A′DE,由平行线的性质可得,A′E⊥AC,通过图形进行计算即可解答.
解:∵C=90°,AB=5,BC=4,∴AC=3,
①当A′点在直线AB的上方时,如图所示,
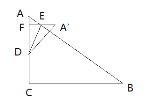
∵△ADE沿DE翻折后,A′E∥BC,
∴△ADE≌△A′DE,∴AD= A′D=![]() ,cos∠A= cos∠A′,
,cos∠A= cos∠A′,
则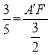 ,可得,A′F=
,可得,A′F=![]() , sin∠A= sin∠A′,可得DF=
, sin∠A= sin∠A′,可得DF=![]() ,
,
∴AF=AD-DF=![]() ,
,
cos∠A=![]() =
=![]() ,解得AE=
,解得AE=![]() ;
;
②当A′点在直线AB的下方时,如图所示,
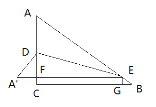
同理可得,AD= A′D=![]() ,A′F=
,A′F=![]() , DF=
, DF=![]() ,
,
∴CF=AC-AD-DF=![]() ,
,
∵四边形EFCG是矩形,∴EG=CF=![]() ,
,
sin∠B=![]() ,解得EB=
,解得EB=![]() ,
,
∴AE=AB-EB=![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
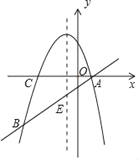
【题目】如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.
(1)求抛物线的解板式.
(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.
(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,B的坐标分别为(-4,5),(-2,1).

(1)写出点C及点C关于y轴对称的点C′的坐标;
(2)请作出△ABC关于y轴对称的△A′B′C′;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
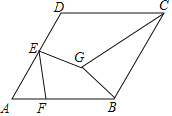
【题目】如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边BC上的一个动点,EG=EF,且∠GEF=60°,则GB+GC的最小值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】母亲节前,某淘宝店从厂家购进某款网红礼盒,已知该款礼盒每个成本价为30元.经市场调查发现,该礼盒每天的销售量y(个)与销售单价x(元)之间满足一次函数关系.当该款礼盒每个售价为40元时,每天可卖出300个;当该款礼盒每个售价为55元时,每天可卖出150个.
(1)求y与x之间的函数解析式(不要求写出x的取值范围);
(2)若该店老板想达到每天不低于240个的销售量,则该礼盒每个售价定为多少元时,每天的销售利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
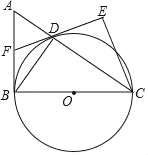
【题目】如图,已知直角△ABC中,∠ABC=90°,BC为圆O的直径,D为圆O与斜边AC的交点,DE为圆O的切线,DE交AB于F,且CE⊥DE.
(1)求证:CA平分∠ECB;
(2)若DE=3,CE=4,求AB的长;
(3)记△BCD的面积为S1,△CDE的面积为S2,若S1:S2=3:2.求sin∠AFD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
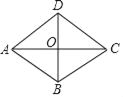
A. 当AB=BC时,平行四边形ABCD是菱形
B. 当AC⊥BD时,平行四边形ABCD是菱形
C. 当AC=BD时,平行四边形ABCD是正方形
D. 当∠ABC=90°时,平行四边形ABCD是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com