
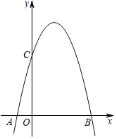
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴交于A,B两点(点A在原点左侧,点B在原点右侧),与y轴交于点C,已知OA=1,OC=OB.
(1)求抛物线的解析式;
(2)若D(2,m)在该抛物线上,连接CD,DB,求四边形OCDB 的面积;
(3)设E是该抛物线上位于对称轴右侧的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点E作EH⊥x轴于点H,再过点F作FG⊥x轴于点G,得到矩形EFGH.在点E运动的过程中,当矩形EFGH为正方形时,求出该正方形的边长.
【答案】(1)y=﹣x2+3x+4.;(2)16;(3)正方形的边长为![]() 或
或![]() .
.
【解析】
(1)先求出点C的坐标,则B的坐标即可求得,利用待定系数法即可求得抛物线的解析式;
(2)求出D的坐标,作DM⊥x轴于点E.则S四边形OCDB=S梯形OCDM+S△BMD,利用C、D的坐标即可求出四边形OCDB的面积;
(3)分两种情况考虑,当点E在x轴上方和下方,根据E和F关于对称轴对称,然后利用正方形的性质即可列方程求解.
解:(1)在y=ax2+bx+4中,令x=0,得y=4,则点C的坐标是(0,4).
∵OC=OB,
∴B的坐标是(4,0).
∴抛物线的解析式为y=﹣x2+3x+4.
(2)∴点D(2,m)在抛物线y=﹣x2+3x+4上,
∴﹣4+6+4=m,解得m=6.所以D(2,6).
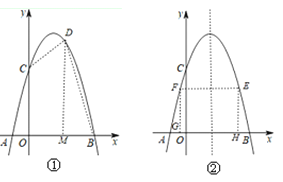
作DM⊥x轴于点M,如图①所示.
则S四边形OCDB=S梯形OCDM+S△BMD=![]() ×(4+6)×2+
×(4+6)×2+![]() ×2×6=10+6=16.
×2×6=10+6=16.
(3)∵抛物线的解析式为y=﹣x2+3x+4,
∴抛物线的对称轴是x=﹣![]() .
.
如图②,设点E的坐标为(x,-x2+3x+4),则点F的坐标为(3-x,-x2+3x+4),EF= x-(3-x)=2x-3.
∵四边形EFGH是正方形,
∴EF=EH.
当E在x轴上方时,2x-3=-x2+3x+4,解得x1=![]() ,x2=
,x2=![]() (舍去)
(舍去)
∴EF=![]() ;当E在x轴下方时,2x-3=-(-x2+3x+4),解得x1=
;当E在x轴下方时,2x-3=-(-x2+3x+4),解得x1=![]() ,x2=
,x2=![]() (舍去).
(舍去).
∴EF=![]() .所以正方形的边长为
.所以正方形的边长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中两条直线OC⊥BC,垂足为C,其OC=2cm,∠COB=60°,反比例函数y=![]() 的图象过点C.
的图象过点C.
(1)求:反比例函数表达式和点B的坐标.
(2)若现有长为1cm的线段MN在线段OB上沿OB方向以1cm/s的速度向点B运动(运动前点M与点O重合,N到点B停止运动),过M、N作OB的垂线分别交直线OC、BC于P、Q两点,线段MN运动的时间为ts.
①若△OMP的面积为S.求出当0<t≤1时,S与t的函数关系式.
②线段MN运动过程中,四边形MNQP有可能成为矩形吗?若可能,直接写出此时t的值;若不可能,说明理由.
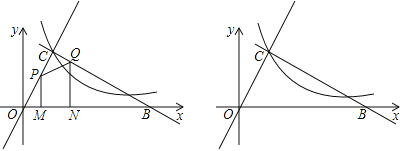
查看答案和解析>>
科目:初中数学 来源: 题型:
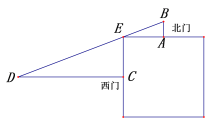
【题目】我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?” .其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B出有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,求正方形城池的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
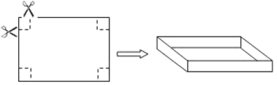
【题目】如图,把一张长![]() ,宽
,宽![]() 的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)要使长方体盒子的底面积为![]() ,求剪去的正方形的边长;
,求剪去的正方形的边长;
(2)你觉得折合而成的长方体盒子的侧面积会不会有更大的情况?如果有,请求出侧面积的最大值和此时剪去的正方形的边长;如果没有,请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论 ①a+b+c<0②a﹣b+c<0③b+2a<0④abc>0⑤b2<4ac,其中正确的个数是( )
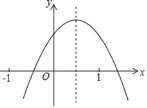
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(m+1)x2﹣(m+3)x+2=0.
(1)证明:当m≠﹣1时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某二次函数图象的顶点坐标为(1,-4),且经过点C(0,-3)
(1)求这个二次函数的表达式;
(2)求图象与x轴交点A、B两点的坐标(A在点B的左边)及△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com